乘法运算定律

　　教学目标：

　　1．引导学生探索和理解乘法交换律、结合律和分配律，能运用运算定律进行一些简便计算。

　　2．培养学生根据具体情况，选择算法的意识与能力，发展思维的灵活性。

　　3．使学生感受数学与现实生活的联系，能用所学知识解决简单的实际问题。

　　教学重点：

乘法交换律、结合律和分配律的学习。

　　教学难点：

乘法交换律、结合律和分配律在计算中的应用。

　　教学过程：

第一课时

　　一、引入新课

　　1.根据运算定律填空。

（1）165＋126＝126＋（             ）

（2）（316＋73）＋127＝316 ＋ （        ＋        ）

2.同学们，听，这整齐的步伐，那优美的旋律，是谁在为我们奏乐呢？（课件出示：鼓号方队的画面）

师：从图中你获取了哪些信息，

生1：我看到了每排都有9个人，有4排。

生2：我发现有9列队员，每列都有4人。

师：你想提出什么数学问题？

生：这个鼓号队里一共有多少个队员？

师：根据所给的信息，你想到了几种计算方法？

生：9×4=36；4×9=36

师：你们真会动脑筋。那么请仔细观察这两个算式，你会有哪些重大的发现呢？

生：两个因数的位置交换了，可它们的积不变。

师：观察真仔细，同学们真了不起，你们的发现非常重要！生活中这样的数学问题还有吗，让我们一起去找找例子！（课件出示主题图）

 

　　二、新课学习乘法交换律

　　师：看他们热火朝天的植树真辛苦啊。你能提出什么数学问题吗？

生： 学生交流、汇报，教师选择记录。

　　师：我们来解决这个问题（课件：负责挖坑、种树的一共有多少人？）

　　师：可以怎样列式呢？

25×4○4×25

　　师：观察这两个算式，你又发现了什么？

　　也就是说25×4和4×25的结果是一样的，都是100.那也就是说这两个算式可以用等号连接。

25×4＝4×25

　　你还能写出类似的算式吗？

　　例如：86×4＝4×86，100×33＝33×100

　　观察这些算式，你能用一句话说一说这个规律吗？

　　让学生用自己的语言说一说，主要是说的清楚，理解规律，不要求一字不差。教师总结：交换两个因数的位置，积不变。

这个规律是不是听起来很耳熟，你能给它起个名字吗？

课件演示：

这就是乘法交换律。你能用字母表示吗？课件演示：

　　三、巩固练习

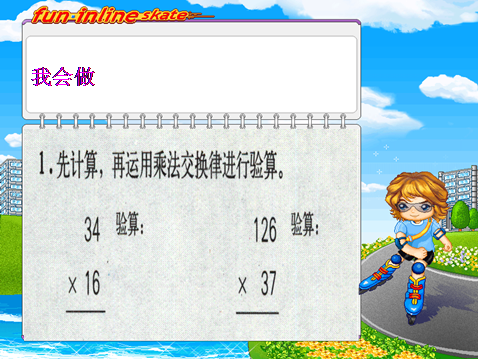
　　（1）26×8＝（    ）×（    ）

（2）56×（    ）＝35×（    ）

　　四、课堂总结

说一说今天你有什么收获？

 

 

 

 

 

第二课时

一、 引入新课

1. 回顾出示课件：

2. 师：根据所给的信息和问题，你想到了哪种解决的好办法？

3.生1：4×9×5    生2： 4×5×9      生3： 9×（4×5）

=36×5           =20×9              =9×20

              =180             =180                =180

4.师：你觉得他们的方法怎样，谈谈你的看法。

生：虽然算式不一样，但只是三个因数所在的位置不一样，运算顺序也就不太一样，可是结果还是相同的！

生：前两个同学的方法都是先算前两个数的积，再和另外一个相乘；后一位同学的是把后两个行相乘再同第一个相乘，这样计算比较简便。因为大家的积都没有变！

师：你与众不同的见解真是让人耳目一新呀！太了不起了！下面我们再看看书本的另外一个问题！

二、 新课学习

师：接下来我们来解决另外一个问题：一共要浇多少桶水？ 课件：

　　可以怎样列式呢？

25×5×2

　　请你算一算，看看谁的方法比较巧妙。

　　观察这两个算式，你发现了什么？

　　师：事实证明无论先计算哪两个数的积，最后的结果是一样的，那也就是说这两个算式可以用等号连接。

（25×5）×2＝25×（5×2）

　　    但是在不改变运算结果的前提下，有时候改变运算顺序会让我们的计算变得简便。

　　你还能写出类似的算式吗？

　　例如：

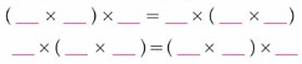
　　观察这些算式，你能用一句话说一说这个规律吗？

　　让学生用自己的语言说一说，主要是说的清楚，理解规律，不要求一字不差。教师总结：先乘前两个数，或者先乘后两个数，积不变。

　　你能给这个规律起个名字吗？

这就是乘法结合律。）课件出示：

也就是说把能够让计算变得简便的两个数先结合起来相乘，再乘第三个数，这样就能算的又对又快。

课件：

三、巩固练习（课件出示练习）

　　2.怎样简便怎样算

　　17×25×4    125×29×8

3.比较加法交换律和乘法交换律、加法结合律与乘法续建结合律，你发现了什么？

　四、课堂总结：

这节课你学到了什么？有什么收获？和大家交流一下。

五、加强练习

 

 

 

 

 

 

 

 

 

 

第三课时

　　一、引入新课

　　师：还记得们知道了乘法的那些运算律吗？谁来说一说。

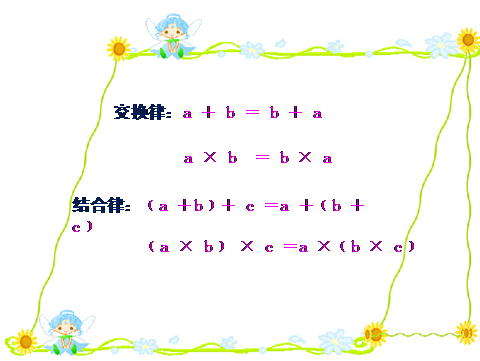
　　生1：乘法交换律：a×b＝b×a

生2：乘法结合律：（a×b）×c＝a×(b×c)

师：出示课件：

 

　　今天我们来继续探究乘法的运算定律，看看是不是还有什么新的规律。

　　二、新课学习

1．算一算。出示课件题目：

生：分角色计算（男生计算左边三道，女生计算右边三道）后上台计算过程和结果。

师：从刚才的计算中，你发现了什么？

生：小组交流自己的看法。

小结：左右两边的算式结果一样。

3． 还是来解决生活中经常出现的下面几个问题：

（1）放映课件：

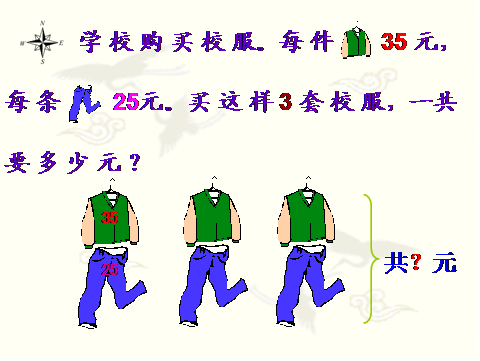
师：你能想出几种解答方法？（与同伴说说你打算先算什么，再算什么？再列式计算）

生：（35 + 25）×3             生：35×3 + 25×3

   = 60 × 3                      = 105 + 75

  = 180（元）                     = 180（元）

答：一 共 要 180 元 。

引导学生发现：（35 + 25）×3 =  35×3 + 25×3，并结合课件演示。

（2）一共有多少名同学参加了这次植树活动？

　　一共有25组，每组里4个人挖坑种树，2个人抬水浇水。那么可以怎样列式呢？请你算一算，看看谁的方法比较巧妙。

　　教师巡视，然后挑出做法比较典型的学生汇报。全班讨论（4＋2）×25和4×25＋2×25的相同和不同之处。

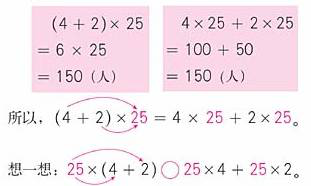
　　观察上面的算式，你发现了什么？

（4＋2）×25＝4×25＋2×25

　　    但是在不改变运算结果的前提下，有时候改变运算顺序会让我们的计算变得简便。

　　让学生用自己的语言说一说，主要是说的清楚，理解规律，不要求一字不差。教师总结：也就是说两个数的和一个数相乘，可以先把它们与这个数分别相乘，再相加。

　　你能给这个规律起个名字吗？

　　这就是乘法分配律。

　　你能用字母表示吗？

（a＋b）×c＝a×c＋a×c

或者：a×（b＋c）＝a×b＋a×c

　　三、巩固练习

播放课件：

 

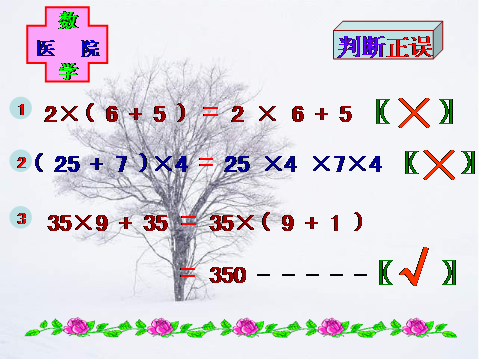
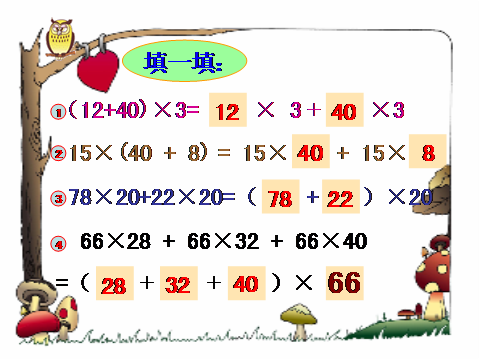
　　四、课堂总结

　　    我们学习了乘法的交换律、结合律还有分配律，合理应用这些规律会让计算变得简便。