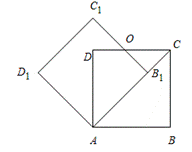
原创模拟预测题1. 如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB₁C₁D₁，边B₁C₁与CD交于点O，则四边形AB₁OD的面积是（）

A．     B．    C．    D．

【答案】C．

【解析】

试题分析：连接AC₁，AO，根据四边形AB₁C₁D₁是正方形，得出∠C₁AB₁=∠AC₁B₁=45°，求出∠DAB₁=45°，推出A、D、C₁三点共线，在Rt△C₁D₁A中，由勾股定理求出AC₁，进而求出DC₁=OD，根据三角形的面积计算即可．

试题解析：连接AC₁，

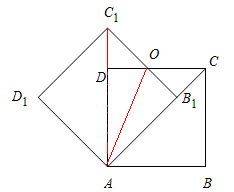
∴∠DAB₁=90°-45°=45°，

∴AC₁过D点，即A、D、C₁三点共线，

故选C．

考点：1．旋转的性质；2．正方形的性质．

 

原创模拟预测题2. 如图，已知l₁∥l₂∥l₃，相邻两条平行直线间的距离相等，若Rt△ABC的三个项点分别在这三条平行直线上，且∠ACB=90°，∠ABC=30°，则cosα的值是【    】

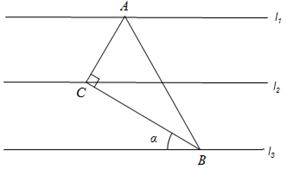
A.           B.          C.         D.

【答案】D。

【考点】平行线的性质，相似三角形的判定和性质，勾股定理，锐角三角函数定义，特殊角的三角函数值。

【分析】如图，分别过点C作DE⊥l₂， DE与l₁交于点D，DE与l₃交于点E，

            

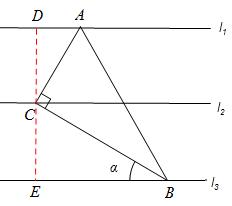
故选D。

原创模拟预测题3. 如图，以矩形ABCD的对角线AC的中点O为圆心、OA长为半径作⊙O，⊙O经过B、D两点，过点B作BK⊥AC，垂足为K，过点D作DH∥KB，DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H。

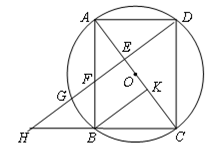
（1）求证：AE＝CK

（2）若AB＝a，AD＝a（a为常数），求BK的长（用含a的代数式表示）。

（3）若F是EG的中点，且DE＝6，求⊙O的半径和GH的长。

【答案】（1）证明见解析；（2）；（3），6．

【解析】

试题解析：（1）证明：∵四边形ABCD是矩形，

∴AD∥BC，AD=BC，

∴∠DAE=∠BCK，

∵BK⊥AC，DH∥KB，

∴∠BKC=∠AED=90°，

∴△BKC≌△ADE，

∴AE=CK；

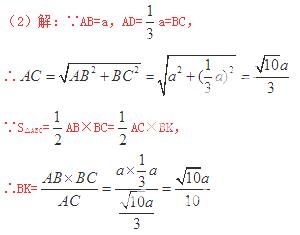
（3）连结OG，

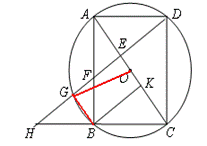
∵AC⊥DG，AC是⊙O的直径，DE=6，∴DE=EG=6，

又∵EF=FG，∴EF=3；

连接BG可得△BGF≌△AEF，AF=BF，△ADF≌△BHF

∵AD=BC，BF∥CD，∴HF=DF，

∵FG=EF，∴HF-FG=DF-EF，∴HG=DE=6．

考点：1．相似三角形的判定与性质；2．全等三角形的判定与性质；3．三角形中位线定理；4．垂径定理．

 

原创模拟预测题4. 平面内有四个点A、B、C、D，其中∠ABC=150⁰，∠ADC=30⁰，AB=BC=1，则满足题意的BD长的最大值是    ▲    。

【答案】。

【考点】圆周角定理，圆内接四边形的性质，等腰三角形的性质，勾股定理，二次根式化简。

【分析】如图，考虑到∠ABC=150⁰，∠ADC=30⁰，根据圆内接四边形对角互补的性质，知点A、B、C、D在同一圆上，且点D在优弧AC上，所以BD长的最大值是BO的延长线与⊙O的交点（点O是AB和BC中垂线的交点）。

连接OC，过点C作CH⊥BD于点H，

设OC=x，

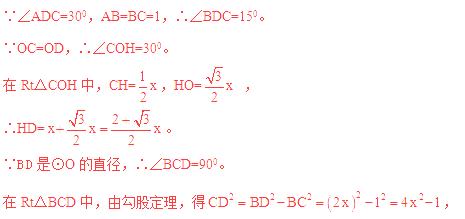
在Rt△CHD中，由勾股定理，得，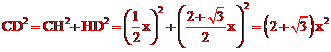

∴。

∴。

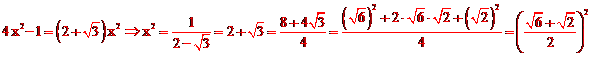∴BD长的最大值是。

原创模拟预测题5. 如图，分别以Rt△ABC的斜两条直角边为边向△ABC外作等边△BCD和等边△ACE， AD与BE交于点H，∠ACB=90°。

（1）求证：AD=BE；

（2）求∠AHE的度数；

（3）若∠BAC=30°，BC=1，求DE的长

【答案】（1）∵△BCD和△ACE是等边三角形，

∴∠BCD=∠ACE=60°，BC=DC，AC=CE。

∴∠ACD=∠ECB。

∴△ACD≌△ECB（SAS）。

∴AD=BE。

【考点】等边三角形的性质，含30度角的直角三角形的性质，圆周角定理，全等三角形的判定和性质，勾股定理。

【分析】（1）由SAS证明△ACD≌△ECB即可。

（2）由（1）得∠DAC=∠BEC，可判定点A、H、C、E在同一圆上，根据圆周角定理即可求得结果。

（3）首先由含30度角的直角三角形的性质求出AB和AC的长，再判定△ABE是直角三角形，由勾股定理得到BE的长，最后由△BCE≌△DCE得出结果。

原创模拟预测题6. 如图，AB为⊙O的直径，弦CD与AB相交于E，DE=EC，过点B的切线与AD的延长线交于F，过E作EG⊥BC于G，延长GE交AD于H．

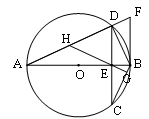
（1）求证：AH=HD；

（2）若AE:AD=，DF=9，求⊙O的半径。

【答案】（1）证明见解析；（2）10．

【解析】

∴AB⊥CD，

∴∠C+∠CBE=90°，

∵EG⊥BC，

∴∠C+∠CEG=90°，

∴∠CBE=∠CEG，

∵∠CBE=∠CDA，∠CEG=∠DEH，

∴∠CDA=∠DEH，

∴HD=EH，

∵∠A+∠ADC=90°，∠AEH+∠DEH=90°，

∴AH=EH，

∴AH=HD；

∴AB=，

∴⊙O的半径为10．

考点：1．切线的性质；2．垂径定理；3．圆周角定理；4．相似三角形的判定与性质．

 

原创模拟预测题7. 如图，A，P，B，C是⊙O上的四个点，∠APC=∠BPC=60°，过点A作⊙O的切线交BP的延长线于点D．

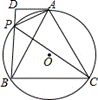
（1）求证：△ADP∽△BDA；

（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；

（3）若AD=2，PD=1，求线段BC的长．

【答案】（1）证明详见解析；（2） PA+PB=PC，证明详见解析；（3）．

【解析】

试题分析：（1）首先作⊙O的直径AE，连接PE，利用切线的性质以及圆周角定理得出∠PAD=∠PBA进而得出答案；

（2）首先在线段PC上截取PF=PB，连接BF，进而得出△BPA≌△BFC（AAS），即可得出PA+PB=PF+FC=PC；

（3）利用△ADP∽△BDA，得出，求出BP的长，进而得出△ADP∽△CAP，则，则AP²=CP•PD求出AP的长，即可得出答案．

（3）解：∵△ADP∽△BDA，∴==，

∵AD=2，PD=1∴BD=4，AB=2AP，∴BP=BD﹣DP=3，

∵∠APD=180°﹣∠BPA=60°，∴∠APD=∠APC，

∵∠PAD=∠E，∠PCA=∠E，∴PAD=∠PCA，∴△ADP∽△CAP，∴=，

∴AP²=CP•PD，∴AP²=（3+AP）•1，

解得：AP=或AP=（舍去），∴BC=AB=2AP=1+．

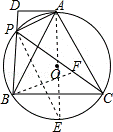
考点：切线的性质；圆周角定理；全等三角形的判定和性质；相似三角形的判定和性质．