| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-8-11 11:21:57 | 点击次数:695次 |
《中考压轴题全揭秘》第二辑 原创模拟预测题
专题21:几何三大变换问题之平移问题
轴对称、平移、旋转是平面几何的三大变换。平移变换是指在同一平面内,将一个图形(含点、线、面)整体按照某个直线方向移动一定的距离,这样的图形变换叫做图形的平移变换,简称平移。平移由两大要素构成:①平移的方向,②平移的距离。平移有如下性质:
1、经过平移,平移前后图形的形状、大小不变,只是位置发生改变,即平移前后的图形全等;
2、平移前后图形的对应点所连的线段平行且相等;
3、平移前后图形的对应线段平行且相等,对应角相等。
中考压轴题中平移问题,包括直线(线段)的平移问题;曲线的平移问题;三角形的平移问题;四边形的平移问题;其它曲面的平移问题。
一. 直线(线段)的平移问题
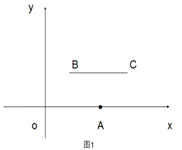
原创模拟预测题1. 定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段与线段的距离.
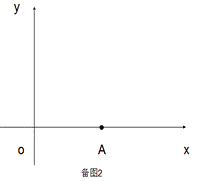
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角系中四点.
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是_____,
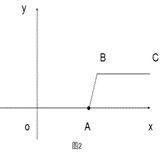
当m=5,n=2时,如图2,线段BC与线段OA的距离(即线段AB的长)为______
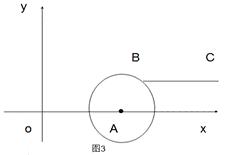
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
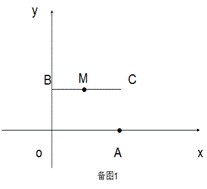
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M.
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值,使以A、M、H为顶点的三角形与△AOD相似,若存在,求出m的值;若不存在,请说明理由.
【答案】(1)2;![]() (2)
(2)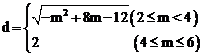 (3)①16+4π②存在,m=1,m=3,m=
(3)①16+4π②存在,m=1,m=3,m=![]()
【解析】解:(1)2;![]() 。
。
(2)∵点B落在圆心为A,半径为2的圆上,∴2≤m≤6。
当4≤m≤6时,根据定义, d=AB=2。
当2≤m<4时,如图,过点B作BE⊥OA于点E,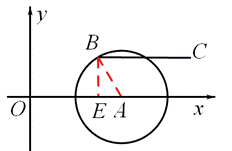
则根据定义,d=EB。

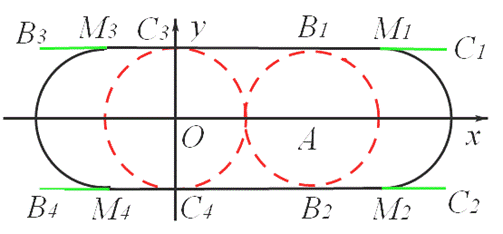
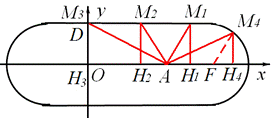
②存在。如图,
由A(4,0),D(0,2), 得![]() 。
。

又FM4=2,∴![]() 。
。
若△AOD∽△A H2M2,则![]() ,即
,即![]() ,
,
解得![]() (不合题意,舍去)。此时m=
(不合题意,舍去)。此时m=![]() 。
。
若△AOD∽△M2H2 A,则![]() ,即
,即![]() ,
,
解得![]() (不合题意,舍去)。
(不合题意,舍去)。

原创模拟预测题2. 把直线![]() 沿y轴方向平移m个单位后,与直线
沿y轴方向平移m个单位后,与直线![]() 的交点在第二象限,则m的取值范围是【 】
的交点在第二象限,则m的取值范围是【 】
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C。
【考点】一次函数图象与平移变换,平面直角坐标系中各象限点的特征,解一元一次不等式组。
 根据平面直角坐标系中各象限点的特征,判断其所在象限,四个象限的符号特征分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)。
根据平面直角坐标系中各象限点的特征,判断其所在象限,四个象限的符号特征分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)。
∵交点在第二象限,∴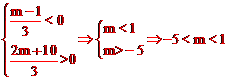 。
。
故选C。
二. 曲线的平移问题
原创模拟预测题3. 定义:如果一个y与x的函数图象经过平移后能与某反比例函数的图象重合,那么称这个函数是y与x的“反比例平移函数”.例如:![]() 的图象向左平移2个单位,再向下平移1个单位得到
的图象向左平移2个单位,再向下平移1个单位得到![]() 的图象,则
的图象,则![]() 是y与x的“反比例平移函数”.
是y与x的“反比例平移函数”.
(1)若矩形的两边分别是2cm、3cm,当这两边分别增加x(cm)、y(cm)后,得到的新矩形的面积为8cm2,求y与x的函数表达式,并判断这个函数是否为“反比例平移函数”.
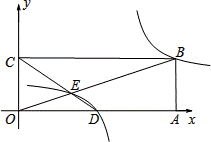
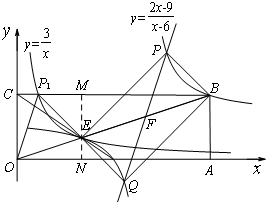
(2)如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A、C的坐标分别为(9,0)、(0,3).点D是OA的中点,连接OB、CD交于点E,“反比例平移函数”![]() 的图象经过B、E两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
的图象经过B、E两点.则这个“反比例平移函数”的表达式为 ;这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合,请写出这个反比例函数的表达式.
(3)在(2)的条件下,已知过线段BE中点的一条直线l交这个“反比例平移函数”图象于P、Q两点(P在Q的右侧),若B、E、P、Q为顶点组成的四边形面积为16,请求出点P的坐标.
【答案】(1)![]() ,是;(2)
,是;(2)![]() ,
,![]() ;(3)(7,5)或(15,
;(3)(7,5)或(15,![]() ).
).
【解析】

(2)把B和D的坐标代入![]() 得:
得: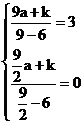 ,解得:
,解得:![]() .
.
则“反比例平移函数”的表达式为![]() .
.
故变换后的反比例函数表达式为![]() .
.

当点P在点B右侧时,同理可得点P的坐标为(15,![]() ).
).
综上所述,点P的坐标为(7,5)或(15,![]() ).
).
考点:1.反比例函数综合题;2.新定义;3.平移的性质;4.转换思想和分类思想的应用.
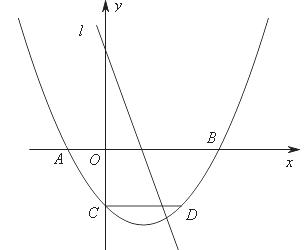
原创模拟预测题4. 如图,抛物线![]() 关于直线
关于直线![]() 对称,与坐标轴交于A、B、C三点,且AB=4,点D
对称,与坐标轴交于A、B、C三点,且AB=4,点D![]() 在抛物线上,直线是一次函数
在抛物线上,直线是一次函数![]() 的图象,点O是坐标原点。
的图象,点O是坐标原点。
(1)求抛物线的解析式;
(2)把抛物线向左平移1个单位,再向上平移4个单位,所得抛物线与直线交于M、N两点,问在y轴负半轴上是否存在一定点P,使得不论k取何值,直线PM与PN总是关于y轴对称?若存在,求出P点坐标;若不存在,请说明理由.
【答案】(1)∵抛物线![]() 关于直线x=1对称,AB=4,∴A(-1,0),B(3,0) 。
关于直线x=1对称,AB=4,∴A(-1,0),B(3,0) 。
∴可设抛物线的解析式为![]() 。
。
∵点D![]() 在抛物线上,∴
在抛物线上,∴![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为![]() ,即
,即![]() 。
。
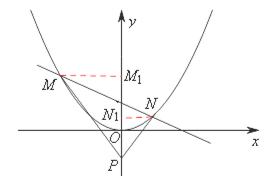
(2)∵![]() ,
,
∴把抛物线向左平移1个单位,再向上平移4个单位,所得抛物线的解析式为![]() 。
。
假设在y轴上存在一点P(0,t),t<0,使直线PM与PN关于y轴对称,过点M、N分别向y轴作垂线MM1、NN1,垂足分别为M1、N1,
∵∠MPO=∠NPO,∴Rt△MPM1∽Rt△NPN1。
∴![]() ………①。
………①。
不妨设M(xM,yM)在点N(xN,yN)的左侧,
因为P点在y轴负半轴上,则①式变为![]() 。
。
又∵![]() ,
,
∴![]() ………②。
………②。
把![]() 代入
代入![]() 中,整理得
中,整理得![]() 。
。
∴![]() ,代入②得
,代入②得![]() ,解得
,解得![]() ,符合条件。
,符合条件。
∴在y轴负半轴上存在一点P(0,![]() ),使直线PM与PN总是关于y轴对称。
),使直线PM与PN总是关于y轴对称。
【考点】二次函数综合题,平移和轴对称问题,待定系数法的应用,曲线上点的坐标与方程的关系,二次函数的性质,一元二次方程根与系数的关系。

三. 三角形的平移问题
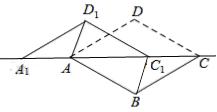
原创模拟预测题5. 如图,将菱形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:
①△A1AD1≌△CC1B;
②当四边形ABC1D1是矩形时,x=![]() ;
;
③当x=2时,△BDD1为等腰直角三角形;
④![]() (0<x<
(0<x<![]() )。
)。
其中正确的是 ▲ (填序号)。
【答案】①②③④。
【考点】平移的性质,菱形的性质,全等三角形的判定,矩形的的判定,等腰直角三角形的判定,含30度直角三角形的性质。
【分析】①∵四边形ABCD为菱形,∴BC=AD,∠ACB =∠DAC。∴∠DAC=∠ACB。
∵把△ACD沿CA方向平移得到△A1C1D1,∴∠A1=∠DAC,A1D1=AD,AA1=CC1。
在△A1AD1与△CC1B中,∵AA1=CC1,∠A1=∠ACB,A1D1=CB,
∴△A1AD1≌△CC1B(SAS)。
故①正确。

②如图1,过点B作BH⊥AC于点H,
∵四边形ABC1D1是矩形,∠AC1D1=∠ACD=∠ACB=30°,
∴∠AC1B=60°。
∴∠C1BC=∠C1CB=30°。∴BC1= CC1=x。
∵AB=BC=2,∴BH=1,HC=![]() 。
。
∴HC1=![]() 。
。
∵HC=HC1+ CC1,∴![]() ,解得
,解得![]() 。
。
故②正确。
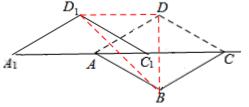
③如图2,根据平移的性质,DD1=CC1=2,∠BDD1=90°,
根据菱形的性质和∠ACB=30°,可得DB=AB=2,
∴DD1= DB=2。
∴△BDD1为等腰直角三角形。
故③正确。
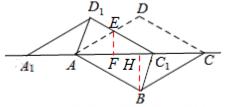

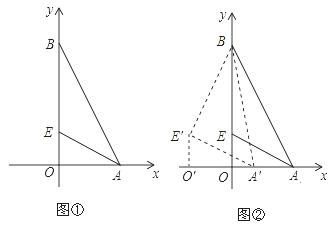
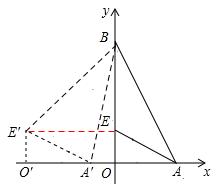
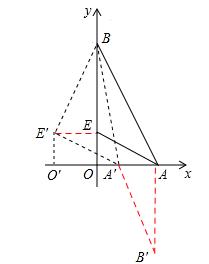
原创模拟预测题6. 如图①,在平面直角坐标系中,已知点A(2,0),点B(0,4),点E(0,1),如图②,将△AEO沿x轴向左平移得到△A′E′O′,连接A′B、BE′。
(1)设AA′=m(m >0),试用含m的式子表示![]() ,并求出使
,并求出使![]() 取得最小值时点E′的坐标;
取得最小值时点E′的坐标;
(2)当A′B+BE′取得最小值时,求点E′的坐标。
【答案】(1)①若0<m<2,如图1,连接EE′,
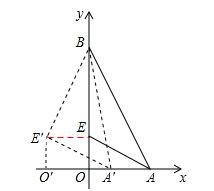
∵点A(2,0),∴A′O=2-m。
在Rt△A′BO中,由![]() ,得
,得
![]() 。
。
∵△A′E′O′是△AEO沿x轴向左平移得到的,
∴EE′∥AA′,且EE′=AA′。∴∠BEE′=90°,EE′=m。
又∵点B(0,4),点E(0,1),∴BE=OB-OE=3。
∴在Rt△BE′E中,![]() 。
。
∴![]() 。
。
又∵![]() ,
,
∴当m=1时,![]() 取得最小值,最小值为27,此时,点E′的坐标是(1,1)。
取得最小值,最小值为27,此时,点E′的坐标是(1,1)。

又∵点B(0,4),点E(0,1),∴BE=OB-OE=3。
∴在Rt△BE′E中,![]() 。
。
∴![]() 。
。
又∵![]() ,
,
∴当m≥2时, ![]() 随m的增大而增大,在m=2时,最小值为29,小于27。
随m的增大而增大,在m=2时,最小值为29,小于27。
综上所述,![]() ,
,![]() 取得最小值时点E′的坐标为(1,1)。
取得最小值时点E′的坐标为(1,1)。

【考点】平移问题,相似三角形的判定和性质,平移的性质,勾股定理,二次函数最值,全等三角形的判定和性质,两点之间线段最短的性质。

四. 四边形的平移问题
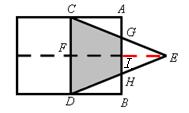
原创模拟预测题7. 如图,矩形的长和宽分别是4和3,等腰三角形的底和高分别是3和4,如果此三角形的底和矩形的宽重合,并且沿矩形两条宽的中点所在的直线自左向右匀速运动至等腰三角形的底与另一宽重合。设矩形与等腰三角形重叠部分(阴影部分)的面积为y,等腰三角形自左向右运动的距离为x,那么y关于x的函数关系式为
。
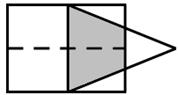
【答案】![]() 。
。
【考点】面动平移问题,由实际问题列函数关系式,相似三角形的判定和性质,梯形面积公式。
【分析】如图,连接IE,

原创模拟预测题8. 已知,大正方形的边长为4,小正方形的边长为2,状态如图所示.大正方形固定不动,把小正方形以的速度向大正方形的内部沿直线平移,设平移的时间为秒,两个正方形重叠部分的面积为,完成下列问题:
(1).用含的式子表示,要求画出相应的图形,表明的范围;
(2).当,求重叠部分的面积;
(3).当,求的值.
【答案】
(1).如图1,当如图2,当如图3,当
(2).当时
答:重叠部分的面积为3
(3).当
答:的值为1.8或4.2

五. 其它曲面的平移问题
原创模拟预测题9. 如图,平面直角坐标系中,⊙O半径长为1.点⊙P(a,0),⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相交时,a值的取值范围为 。
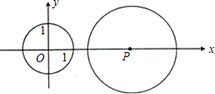
【答案】![]() 或
或![]() 。
。
【考点】两圆的位置关系,平移的性质,分类思想的应用。
【分析】先考虑⊙P与⊙O相切时的情况:
∵⊙O 的圆心在原点,
∴当⊙P与⊙O外切时,圆心距为1+2=3,当⊙P与⊙O内切时,圆心距为2![]() 1=1。
1=1。
∵当⊙P与⊙O第一次外切和内切时,⊙P圆心在x轴的正半轴上,
∴⊙P(3,0)或(1,0)。∴a=3或1。

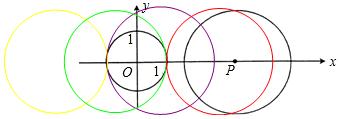
原创模拟预测题10. 如图所示,半径为1的圆和边长为1的正方形在同一水平线上,圆沿该水平线从左向右匀速穿过正方形,设穿过时间为t,正方形除去圆部分的面积为S(阴影部分),则S与t的大致图象为【 】
![]()
A.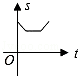 B.
B.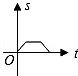 C.
C.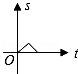 8 D.
8 D.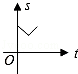
【答案】D。
【考点】动点问题的函数图象。
 原创模拟预测题11.如图,对称轴为
原创模拟预测题11.如图,对称轴为![]() 的抛物线
的抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]()
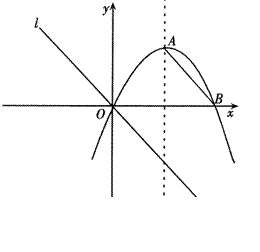
(1).求抛物线的解析式,并求出顶点![]() 的坐标
的坐标
(2).连结AB,把AB所在的直线平移,使它经过原点O,得到直线.点P是上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为,当0<S≤18时,求的取值范围
(3).在(2)的条件下,当取最大值时,抛物线上是否存在点![]() ,使△OP
,使△OP![]() 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】
(1).(3,3)
(2).-3≤![]() <0或0<
<0或0<![]() ≤3.
≤3.
(3).存在,点![]() 坐标为(3,3)或(6,0)或(-3,-9)
坐标为(3,3)或(6,0)或(-3,-9)

(说明:可用对称轴为![]() ,求
,求![]() 值,用顶点式求顶点A坐标.)
值,用顶点式求顶点A坐标.)
(2)设直线AB解析式为y=kx+b.
∵A(3,3),B(6,0),
∴![]() 解得
解得![]() ,
∴
,
∴![]() .
.
∵直线∥AB且过点O,
∴直线解析式为![]() .
.
∵点![]() 是上一动点且横坐标为,
是上一动点且横坐标为,
∴点![]() 坐标为(
坐标为(![]() ).
).

作PM⊥![]() 轴于M,设对称轴与
轴于M,设对称轴与![]() 轴交点为N.
轴交点为N.
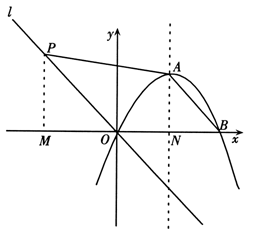
则

=-3![]() +9.
+9.
∵0<S≤18,
∴0<-3![]() +9≤18,
+9≤18,
∴-3≤![]() <3.
<3.
又![]() <0,
<0,
∴-3≤![]() <0.6分
<0.6分
![]()
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

