| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-8-11 11:24:11 | 点击次数:385次 |
《中考压轴题全揭秘》第二辑 原创模拟预测题
专题26:动态几何之面动形成的函数关系问题
数学因运动而充满活力,数学因变化而精彩纷呈。动态题是近年来中考的的一个热点问题,以运动的观点探究几何图形的变化规律问题,称之为动态几何问题,随之产生的动态几何试题就是研究在几何图形的运动中,伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题,就其运动对象而言,有点动、线动、面动三大类,就其运动形式而言,有轴对称(翻折)、平移、旋转(中心对称、滚动)等,就问题类型而言,有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。解这类题目要“以静制动”,即把动态问题,变为静态问题来解,而静态问题又是动态问题的特殊情况。以动态几何问题为基架而精心设计的考题,可谓璀璨夺目、精彩四射。
动态几何形成的函数关系和图象问题是动态几何中的基本问题,包括单动点形成的函数关系和图象问题,双(多)动点形成的函数关系和图象问题,线动形成的函数关系和图象问题,面动形成的函数关系和图象问题。本专题原创编写面动形成的函数关系问题模拟题。
面动问题就是在一些基本几何图形上,设计一个动面(包括平移和旋转),或由点动、线动形成面动,并对面在运动变化的过程中产生的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究
在中考压轴题中,面动形成的函数关系问题的重点和难点在于应用数形结合的思想准确地进行分类。
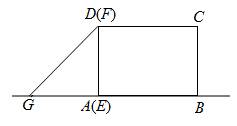
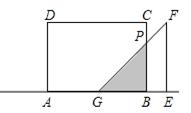
原创模拟预测题1. 如图,点G、E、A、B在一条直线上,等腰直角△EFG从如图所示是位置出发,沿直线AB以1单位/秒向右匀速运动,当点G与B重合时停止运动。已知AD=1,AB=2,设△EFG与矩形ABCD重合部分的面积为S平方单位,运动时间为t秒,则S与t的函数关系是 。
【答案】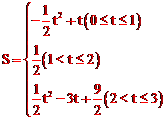 。
。
【考点】面动问题的函数图象,矩形和等腰直角三角形性质,数形结合思想和分类思想的应用。
【分析】分三种情况讨论:
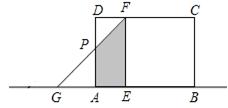
如图1,当点G在点A左侧,点E在点A右侧时, 此时0≤t≤1,
AE= t,![]()
∴![]() 。
。
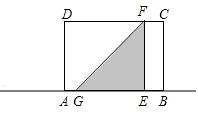
如图2,当点G,E在点A,B之间时, 此时1˂t≤2,
∴![]() 。
。

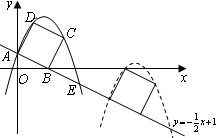
原创模拟预测题2. 如图,已知直线![]() 交坐标轴于
交坐标轴于![]() 两点,以线段
两点,以线段![]() 为边向上作正方形
为边向上作正方形
![]() ,过点
,过点![]() 的抛物线与直线另一个交点为
的抛物线与直线另一个交点为![]() .
.
(1)请直接写出点![]() 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)若正方形以每秒![]() 个单位长度的速度沿射线
个单位长度的速度沿射线![]() 下滑,直至顶点
下滑,直至顶点![]() 落在
落在![]() 轴上时停止.设正方形落在
轴上时停止.设正方形落在![]() 轴下方部分的面积为
轴下方部分的面积为![]() ,求
,求![]() 关于滑行时间的函数关系式,并写出相应自变量的取值范围;
关于滑行时间的函数关系式,并写出相应自变量的取值范围;
【答案】(1)![]() ;(2)
;(2)![]() ;
;
(3)当![]() 时,
时,![]()
当![]() 时,
时, ![]()
![]()
![]() ;
;
当![]() 时,
时,![]() =
=![]() .
.
【解析】

![]() 抛物线过点
抛物线过点![]()
![]() ,
,
![]()
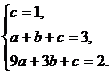 解得
解得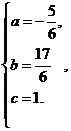
∴![]() ;
;
(3)①当点A运动到点F时,![]()
当![]() 时,如图1,
时,如图1,
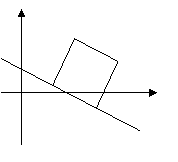
∵![]() ,
,![]()
∴![]()
∴![]()
∴![]() ;
;
②当点![]() 运动到
运动到![]() 轴上时,
轴上时,![]() ,
,
当![]() 时,如图2,
时,如图2,

![]()
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]() ;
;
③当点![]() 运动到
运动到![]() 轴上时,
轴上时,![]() ,
,
当![]() 时,如图3,
时,如图3,
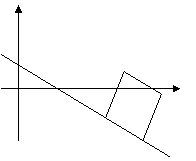
∵![]() ,
,
∴![]()
∵![]()
![]() ,
,
![]()
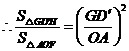 ,
,
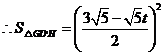 ,
,
∴![]() =
=![]() .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.
原创模拟预测题3. 如图,长是2宽是1的矩形和边长是1的正三角形,矩形的一长边与正三角形的一边在同一水平线上,三角形沿该水平线自左向右匀速穿过矩形。设穿过的时间为t,矩形与三角形重合部分的面积为S,那么S关于t的函数大致图象应为 【 】

A.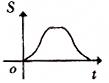 B.
B.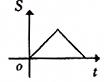 C.
C.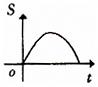 D.
D.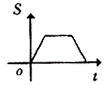
【答案】A。
【考点】动面问题的函数图象,矩形和等边三角形的性质。

故选A。
原创模拟预测题4. 如图,平面之间坐标系中,Rt△ABC的∠ACB=90o,∠CAB=30o,直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=![]() ,经过O,C两点做抛物线
,经过O,C两点做抛物线![]() (a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
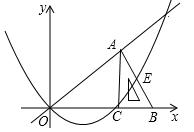
(1)填空:用含t的代数式表示点A的坐标及k的值:A ,k= ;
(2)随着三角板的滑动,当a=1时:
①请你验证:抛物线![]() 的顶点在函数
的顶点在函数![]() 的图象上;
的图象上;
②当三角板滑至点E为AB的中点时,求t的值。
【答案】(1)(t,![]() );
);![]() (k>0)。
(k>0)。
(2)①当a=时1,![]() ,其顶点坐标为
,其顶点坐标为![]() 。
。
对于![]() ,当x=
,当x=![]() 时,
时,![]() 。∴点
。∴点![]() 在抛物线
在抛物线![]() 上。
上。
∴当a=![]() 时,抛物线
时,抛物线![]() 的顶点在函数
的顶点在函数![]() 的图象上。
的图象上。
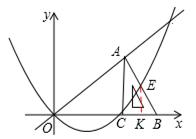
②如图,过点E作EK⊥x轴于点K,
∵直角边AC=![]() ,∴另一直角边CB=2。
,∴另一直角边CB=2。
∵AC⊥x轴,∴AC∥EK。
∵点E是线段AB的中点,∴K为BC的中点。
∴EK是△ACB的中位线。
∴EK=![]() AC=
AC=![]() ,CK=
,CK=![]() CB=1。∴E(t+1,
CB=1。∴E(t+1,![]() )。
)。
∵点E在抛物线![]() 上,∴
上,∴![]() ,解得
,解得![]() 。
。
∴当三角板滑至点E为AB的中点时,![]() 。
。
【考点】面动平移问题,曲线上点的坐标与方程的关系,二次函数的性质,三角形中位线定理,含30度直角三角形的性质。

原创模拟预测题5. 如图(1),Rt△ABC和Rt△EFD中,AC与DE重合,AB=EF=1,∠BAC=∠DEF=90o,∠ ACB=∠EDF=30o,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止。现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线) 于G,H点,如图(2)
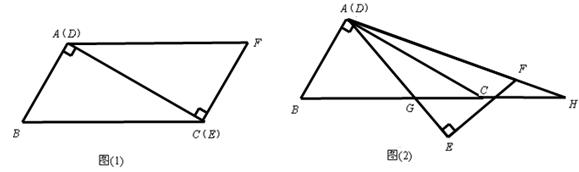
(1)问:始终与△AGC相似的三角形是 ▲ ;
(2)设CG=x,BG=y,求y关于x的函数关系式;
(3)问:当x为何值时,△HGA是等腰三角形。
【答案】(1)△HGA。
(2)∵∠BAC =90o,∠ ACB =30o,AB =1,∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
又∵BC=2,∴![]() 。
。
∴y关于x的函数关系式为![]() 。
。
(3)由(1)知,△AGC∽△HGA,若△HGA是等腰三角形,则AGC也是等腰三角形。所以分两种情况:
①当CG=AG时,AG是Rt△ABC斜边上的中线, 此时,x=CG=![]() BC=1。
BC=1。
②当CG= CA时, x=CG=![]() 。
。
∴当x=1或![]() 时,△AGH是等腰三角形。
时,△AGH是等腰三角形。
【考点】面动旋转问题,含30度角直角三角形的性质,三角形内角和外角性质,相似三角形的判定和性质,等腰三角形的判定,由实际问题列函数关系式,分类思想的应用。

(3)考虑CG=AG和CG= CA两种情况分别求解即可。
原创模拟预测题6. 如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
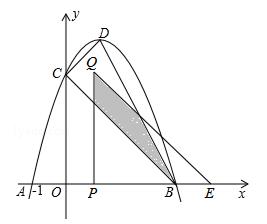
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.


则OM=1,DM=4,BM=OB﹣OM=2。
过点C作CN⊥DM于点N,
则CN=1,DN=DM﹣MN=DM﹣OC=1。
在Rt△OBC中,由勾股定理得:![]() ;
;
在Rt△CND中,由勾股定理得:![]() ;
;
在Rt△BMD中,由勾股定理得:![]() 。
。
∵BC2+CD2=BD2,∴根据勾股定理的逆定理,得△CDB为直角三角形。

∵B(3,0),D(1,4),∴![]() ,解得:
,解得:![]() 。
。
∴直线BD的解析式为y=﹣2x+6。
连接CQ并延长,射线CQ交BD于点G,则G(![]() ,3)。
,3)。
在△COB向右平移的过程中:
①当0<t≤![]() 时,如答图2所示:
时,如答图2所示:
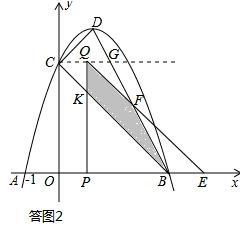
设PQ与BC交于点K,可得QK=CQ=t,PB=PK=3﹣t.

②当![]() <t<3时,如答图3所示,
<t<3时,如答图3所示,

设PQ分别与BC、BD交于点K、点J,
∵CQ=t,∴KQ=t,PK=PB=3﹣t。
直线BD解析式为y=﹣2x+6,令x=t,得y=6﹣2t。∴J(t,6﹣2t)。
∴S=S△PBJ﹣S△PBK=![]() PB•PJ﹣
PB•PJ﹣![]() PB•PK=
PB•PK=![]() (3﹣t)(6﹣2t)﹣
(3﹣t)(6﹣2t)﹣![]() (3﹣t)2=
(3﹣t)2=![]() t2﹣3t+
t2﹣3t+![]() 。
。
综上所述,S与t的函数关系式为:S=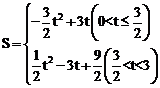 。
。
【解析】

②当![]() <t<3时,如答图3所示,此时重叠部分为一个三角形。
<t<3时,如答图3所示,此时重叠部分为一个三角形。
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

