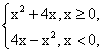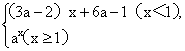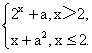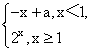课  题

函数的单调性与最值

课  型

讲评课

课  时

第   2   课时

主备课人

周  思

复备课人

陈雄武

审核人

雷淇未

课前准备

教 学 目 标

1．理解函数的单调性，会讨论和证明一些简单的函数的单调性；

 2．理解函数的最大（小）值及其几何意义，并能求出一些简单的函数的最大（小）值

教学重点

求单调区间，判断函数的单调性，求函数的最值或求某变量的取值范围

教学难点

函数的最值

教学过程和教学内容

二次备课

一、基础回扣

1.函数f(x)=|x|和g(x)=x(2-x)的递增区间依次是(　　)

(A)(-∞,0],(-∞,1]      (B)(-∞,0],[1,+∞)

(C)[0,+∞),(-∞,1]      (D)[0,+∞),[1,+∞)

2.给定函数①y=,②y=,③y=|x-1|,

④y=2^x+1,其中在区间(0,1)上是单调递减的函数的序号是(　　)

(A)①②     (B)②③     (C)③④     (D)①④

3.函数f(x)=1-(　　)

(A)在(-1,+∞)上单调递增

(B)在(1,+∞)上单调递增

(C)在(-1,+∞)上单调递减

(D)在(1,+∞)上单调递减

4.(2013·佛山模拟)若函数y=ax与y=在(0,+∞)上都是减函数,则y=ax²+bx在(0,+∞)上是(　　)

(A)增函数                   (B)减函数

(C)先增后减                 (D)先减后增

5.已知函数f(x)=若f(2-a²)>f(a),则实数a的取值范围是

(A)(-∞,-1)∪(2,+∞)

(B)(-1,2)

(C)(-2,1)

(D)(-∞,-2)∪(1,+∞)

6.已知函数f(x)=单调递减,那么实数a的取值范围是(　　)

(A)(0,1)      (B)(0,)   (C)[,)      (D)[,1)

7.定义在R上的函数f(x)在区间(-∞,2)上是增函数,且f(x+2)的图象关于x=0对称,则(　　)

(A)f(-1)          

(C)f(-1)=f(3)           (D)f(0)=f(3)

8.定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)>0,则函数f(x)在[a,b]上有(　　)

(A)最小值f(a)           (B)最大值f(b)

(C)最小值f(b)           (D)最大值f()

9.(2013·天津模拟)设函数f(x)=若f(x)的值域为R,则常数a的取值范围是(　　)

(A)(-∞,-1]∪[2,+∞)    (B)[-1,2]

(C)(-∞,-2]∪[1,+∞)   (D)[-2,1]

10.(能力挑战题)已知函数f(x)是定义在(0,+∞)上的单调函数,若对任意x∈(0,+∞),都有f(f(x)-)=2,则f()的值是(　　)

(A)5        (B)6        (C)7        (D)8

二、填空题

11.函数y=-(x-3)|x|的递增区间是　　　　.

12.(2013·广州模拟)对于任意实数a,b,定义min{a,b}=设函数f(x)=-x+3,g(x)=log₂x,则函数h(x)=min{f(x),g(x)}的最大值是　　　 .

13.设函数f(x)=的最小值为2,则实数a的取值范围是　　　 .

14.(2013·株洲模拟)f(x)=x²-2x(x∈［-2,4］)的单调增区间为　　　 ；f(x)_max=　　　.

三、解答题

15.已知f(x)=(x≠a).

(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.

(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.

四、课时作业 预习金版13-15

教学札记：