| 上传:席俊雄数学 | 审核发布:admin | 更新时间:2015-10-24 9:46:34 | 点击次数:1873次 |
课题: 高考题中的三个超越函数及应用
湖南东安一中 唐志达
一、教学内容分析
导数进入高中数学后,为解决函数的单调性和最值问题提供了简便易行的方法,因而成了每年高考的必考内容,教者在研究历年高考试题中发现,高考题中一些与不等式有关的问题的解决,最终用到下面三个超越函数的单调性和最值,本节课将作介绍,供同学们学习参考。
二、教学目的
1、进一步熟悉利用导数研究函数单调性和极值(最值)的方法;
2、掌握所研究的三个超越函数的单调性和最值;
3、培养学生综合运用数学知识解决问题的能力。
三、教学重点 三个超越函数的单调性及运用。
四、教学难点 三个超越函数单调性的运用。
五、教学过程
1、复习提问
前面我们学习了利用导数研究函数的单调性和极值,解题步骤是怎样的?
【指定学生回答,然后教师总结并板书】
求函数单调区间的步骤是:
①求函数的定义域; ②求![]() ;
;
③解不等式![]() 得f(x)的单调递增区间;
得f(x)的单调递增区间;
解不等式![]() 得f(x)的单调递减区间。
得f(x)的单调递减区间。
求函数极值的步骤是:
①求函数的定义域; ②求![]() =0的根;
=0的根;
③检验![]() 在
在![]() 的根的左右的符号。
的根的左右的符号。
如果![]() 在根的附近左正右负,这个根是极大值点;
在根的附近左正右负,这个根是极大值点;
如果![]() 在根的附近左负右正,这个根是极小值点。
在根的附近左负右正,这个根是极小值点。
2、下面请同学们研究下面三个函数的单调性和极值:
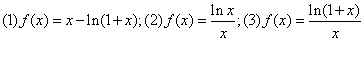 。
。
【请三名同学上黑板先做,然后教师讲评】
解:(1)f(x)的定义域为![]() ,
,![]() 。
。
![]() ,所以f(x)在
,所以f(x)在![]() 是增函数。
是增函数。
![]() 所以f(x)在
所以f(x)在![]() 是减函数。
是减函数。
故当x=0时,f(x)有极小值,极小值为f(0)=0。
(2)f(x)的定义域为![]() ,
,![]()
![]() ,所以f(x)在
,所以f(x)在![]() 是增函数,
是增函数,
![]() ,所以f(x)在
,所以f(x)在![]() 是减函数。
是减函数。
故当x=e时,f(x)有极大值,极大值为f(e)= ![]() 。
。
(3)f(x)的定义域为![]() ,
,![]() 。
。
设![]() 则
则![]() .
.
![]() 所以f(x)在
所以f(x)在![]() 上是增函数,故
上是增函数,故![]() 。
。
此时,![]() 所以
所以![]() 在
在![]() 是减函数。
是减函数。
![]() ,所以g(x)在
,所以g(x)在![]() 是减函数,故
是减函数,故![]() .
.
此时,![]() ,所以
,所以![]() 在
在![]() 是减函数。
是减函数。
故f(x)没有极值。
【然后师生共同总结出下面三个结论】
3、三个有用结论
结论1:函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 是增函数。
是增函数。
推论:![]()
![]() 。
。
结论2:函数![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数。
是减函数。
结论3:函数![]() 在
在![]() 是减函数。
是减函数。
【教师小结:这三个函数是最简单和最常用的三个超越函数,在历年高考试题中直接或者间接地考查这三个超越函数及性质,因而我们一定要掌握它,下面我们来看它们的一些简单应用】
4、例题分析
例1(2005年全国高考)若![]() ,则( )。
,则( )。
A.a
分析:因为![]() 在
在![]() 是增函数,在
是增函数,在![]() 是减函数,
是减函数,
所以![]() ,即
,即![]() 。由于
。由于![]() ,
,
所以b>a>c , 选C。
例2(2001年全国高考)已知m,n为正整数,且1![]()
分析:![]() 时,
时,![]()
![]()
由于函数![]() 在
在![]() 是减函数,又
是减函数,又![]()
所以![]() ,即
,即![]() 成立。 故原不等式成立。
成立。 故原不等式成立。
【教师小结:将数学问题进行等价变形使问题明化,是解决数学难题的常用技巧,同学们要细心体会;数列是定义域为![]() 或它的子集{1,2,3,.. .,n}的特殊函数,因而每一个数列都对应于定义域为
或它的子集{1,2,3,.. .,n}的特殊函数,因而每一个数列都对应于定义域为![]() 或者它的子集的一个函数,因而很多数列问题通过研究数列对应的函数的性质,使数列问题获解是函数应用的一大亮点。】
或者它的子集的一个函数,因而很多数列问题通过研究数列对应的函数的性质,使数列问题获解是函数应用的一大亮点。】
例3(2000年四川高考题)设函数![]() 。
。
(1)当x=6时,求![]() 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(2)对任意的实数x,证明:![]() .
.
分析:(1)x=6时,展开式中二项式系数最大的项是中间项![]() 。
。
(2)![]()
![]() 。
。
![]() ,
,![]() 时,
时,![]() ,
,![]() 。
。
从而![]() ,即
,即![]() .
.
例4已知数列![]() 满足
满足![]()
![]() ,求证:
,求证:![]() .
.
分析:![]() 对一切
对一切![]() 都成立,
都成立,
![]() =
=![]() 。
。
由于x>0时,![]() 。
。
![]()
![]() ,
,
![]()
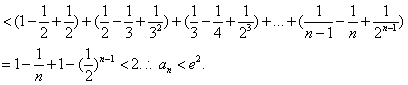
5、课堂小结
本节课我们从复习利用导数求函数单调性和极值(最值)的方法入手,然后研究了三个超越函数![]() ,
,![]() ,
,![]() 的单调性和极值(最值),重点是通过例题来研究这三个超越函数的性质的简单应用,对于数学难题,我们要善于观察题目的条件和结论之间的联系与区别,联想有关的数学知识进行等价转化,进行知识迁移,才能使问题获得解决。
的单调性和极值(最值),重点是通过例题来研究这三个超越函数的性质的简单应用,对于数学难题,我们要善于观察题目的条件和结论之间的联系与区别,联想有关的数学知识进行等价转化,进行知识迁移,才能使问题获得解决。
六、作业
1.(2008年福建省高考题)已知函数![]()
(I) 求函数![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,设
,设![]() ,
,
求证:![]() 。
。
2.(2008年全国高考题改编)已知函数![]()
若对所有的![]() 都有
都有![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
3.(2008年湖南高考题)已知函数![]()
(I) 求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若不等式![]() 对任意的
对任意的![]() 都成立(其中e是自然对数的底数).求a的最大值。
都成立(其中e是自然对数的底数).求a的最大值。
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

