| 上传:席俊雄数学 | 审核发布:admin | 更新时间:2015-10-20 15:29:47 | 点击次数:604次 |
上课时间:2015年 月 日 学期总第 课时
|
课 题 |
函数的单调性与最值 |
课 型 |
讲评课 |
|
|
课 时 |
第 3 课时 |
主备课人 |
陈雄武 |
|
|
复备课人 |
周 思 |
审核人 |
雷淇未 |
|
|
课前准备 |
|
|||
|
教 学 目 标 |
1.理解函数的单调性,会讨论和证明一些简单的函数的单调性; 2.理解函数的最大(小)值及其几何意义,并能求出一些简单的函数的值域 |
|||
|
教学重点 |
判断函数的单调性,求函数的最值或值域 |
|||
|
教学难点 |
|
|||
|
教学过程和教学内容 |
二次备课 |
|||
|
一、典例突破 求下列函数的值域: (1) (3) (4) (6) (7) (9) (11) 解:(1)(配方法) ∴ 改题:求函数 解:(利用函数的单调性)函数 ∴当 ∴函数 (2)求复合函数的值域: 设 又∵ ∴ ∴ (3)(法一)反函数法:
∴原函数 (法二)分离变量法: ∵ ∴函数 (4)换元法(代数换元法):设 ∴原函数可化为 ∴原函数值域为 注:总结 变形: (5)三角换元法: ∵ 则 ∵ ∴ ∴原函数的值域为 (6)数形结合法: ∴ (7)判别式法:∵ 由 ①当 ②当 ∵ ∴△ ∴ ∴原函数的值域为 (8)∵ ∴ 当且仅当 ∴ (9)(法一)方程法:原函数可化为: ∴ ∴ ∴ ∴ ∴ ∴原函数的值域为 (法二)利用 二、课时作业 |
|
|||
|
教学札记: |
||||
东安一中教务处设计
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

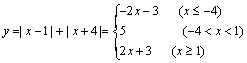

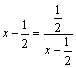 时,即
时,即