课  题

1.1.2集合间的基本关系

课  型

新授课

课  时

         第1课时

主备课人

唐志达

复备课人

将衡山，唐瑞山

执教人

唐志达

课前准备

要求学生预习P6-7

教 学 目 标

知识与技能：1.掌握集合集合间的三种基本关系及其定义，能根据条件写出集合的子集

2.能根据集合间的关系求解集合中的参数问题.

过程与方法：提问，探究，总结，应用巩固，小结.分类讨论思想

情感态度与价值观：培养学生主动探索、敢于实践、勇于发现、合作交流的精神.

教学重点

掌握集合集合间的三种基本关系，能根据条件写出集合的子集

教学难点

能根据集合间的关系求解集合中的参数问题.

教学过程和教学内容

二次备课

一、课前准备

（预习教材P₆~ P₇，找出疑惑之处）

复习1：集合的表示方法有         、        、       . 请用适当的方法表示下列集合.

（1）10以内3的倍数；（2）1000以内3的倍数.

复习2：用适当的符号填空.（1） 0    N；    Q；  -1.5    R.（2）设集合，，则1      A；b     B；      A.

思考：类比实数的大小关系，如5<7，2≤2，试想集合间是否有类似的“大小”关系呢？

二、新课导学※ 学习探究

探究：比较下面几个例子，试发现两个集合之间的关系：

与.

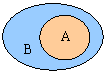
新知：子集、相等、真子集、空集的概念.

① 如果集合A的任意一个元素都是集合B的元素，我们说这两个集合有包含关系，称集合A是集合B的子集（subset），记作：，读作：A包含于（is contained in）B，或B包含(contains)A.

当集合A不包含于集合B时，记作.

①      在数学中，我们经常用平面上封闭曲线的内部代表

集合，这种图称为Venn图. 用Venn图表示两个集合

间的“包含”关系为：.

③ 集合相等：若，则中的元素是一样的，因此.

④ 真子集：若集合，存在元素，则称集合A是集合B的真子集（proper subset），记作：A  B（或B A），读作：A真包含于B（或B真包含A）.

⑤ 空集：不含有任何元素的集合称为空集（empty set），记作：. 并规定：空集是任何集合的子集，是任何非空集合的真子集.

试试1：P7 NO:2，3

反思：思考下列问题.（1）符号“”与“”有什么区别？试举例说明.（2）任何一个集合是它本身的子集吗？任何一个集合是它本身的真子集吗？试用符号表示结论.

（3）类比下列实数中的结论，你能在集合中得出什么结论？

① 若；② 若.

※ 典型例题

例1 写出集合的所有的子集，并指出其中哪些是它的真子集.

变式：1..分别写出集合的所有真子集组成的集合.

2.的子集有     个，非空子集有     个，真子集有     个，非空真子集有     个。

试一试2：P7  NO：1

三、总结提升※ 学习小结

1. 子集、真子集、空集、相等的概念及符号；Venn图图示；一些结论.

2. 两个集合间的基本关系只有“包含”与“相等”两种，可类比两个实数间的大小关系，特别要注意区别“属于”与“包含”两种关系及其表示方法.

※ 知识拓展

如果一个集合含有n个元素，那么它的子集有个，真子集有个.

※ 当堂检测（时量：5分钟 满分：10分）计分：

1. 下列结论正确的是（    ）.

   A. A       B.  C.     D.

2. 设，且，则实数a的取值范围为（    ）.

  A.        B.   C.        D.

3. 若，则（    ）.

  A.    B.  C.     D.

4. 满足的集合A有   个.

5. 设集合，，则它们之间的关系是            ，并用Venn图表示.

 课后作业

P12  NO:5

教学札记：