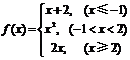课  题

§1.2.2  函数的表示法（3）

课  型

新授

课  时

第3 课时

主备课人

       唐志达

复备课人

周永善

审核人

蒋衡山，唐瑞山

课前准备

教 学 目 标

知识与技能：1.通过具体实例，了解简单的分段函数，并能简单应用.

2. 能解决简单函数应用问题.

过程与方法：学习函数的表示形式，其目的不仅是研究函数的性质和应用的需要，而且是为加深理解函数概念的形成过程．

情感态度与价值观：激发学生的学习热情，激发学生的求知欲，培养严谨的学习态度，培养积极进取的精神．

教学重点

简单的分段函数及应用

教学难点

利用分段函数解决简单的应用问题

教学过程和教学内容

二次备课

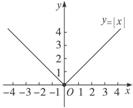
一、 新课导学：

探究任务：分段函数

例1：作出函数的图象和的图象，并分别求出函数的值域。

解法一：由绝对值的概念,我们有y=

所以,函数y=|x|的图象如图1-2-2-10所示.

图1-2-2-10

解法二：画函数y=x的图象,将其位于x轴下方的部分对称到x轴上方,与函数y=x的图象位于x轴上方的部分合起来得函数y=|x|的图象如图1-2-2-10所示.

例2：已知，

①求、的值.

②若，求的值。

③画出函数的图象

例3：某市郊空调公共汽车的票价按下列规则制定：

（1）乘坐汽车5公里以内，票价2元；

（2）5公里以上，每增加5公里，票价增加1元（不足5公里按5公里计算），如果某线路总里程为20公里，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象．

解：设里程为x千米时,票价为y元,根据题意得x∈(0,20］.

由空调汽车票价制定的规定,可得到以下函数解析式:

y=

注意：

①象例1、例2、例3中的函数，称为分段函数．

②分段函数的表示法与意义（一个函数，不同范围的x，对应法则不同）．

三、课堂练习：

1. 已知，则=（   ）

  A. 0    B.    C.    D.无法求

2. 设，若，则x=（  ）

A. 1   B.    C.      D.

3.动点P从单位正方形ABCD顶点A开始运动一周，设沿正方形ABCD的运动路程为自变量x，写出P点与A点距离y与x的函数关系式，并画出函数的图象.

提高练习：画出函数f(x)=|x－1|＋|x＋2|的图象，并写出该函数的值域。

四、课堂小结

本节课学习了:画分段函数的图象;求分段函数的解析式以及分段函数的实际应用.

五、作业布置

教学札记：