课题  27.3  位  似 1 学案 人教版九年级下   　

         

导学目标知识点：了解位似图形及其有关概念，了解位似与相似的联系和区别，掌握位

           似图形的性质．掌握位似图形的画法，能够利用作位似图形的方法将一个图形

           放大或缩小．

 课    时：1课时

导学方法：整理、分析、归纳法

导学过程：

一、自主探究（课前导学）

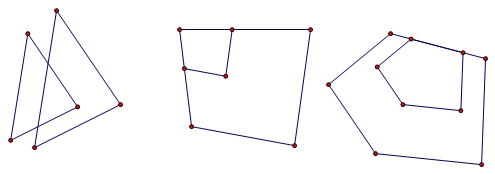
  图中多边形相似吗？观察下面的四个图，你发现每个图中的两个多边形各对应点的连线有什么特征？

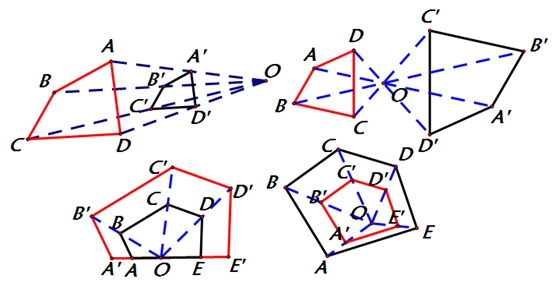
（1）位似图形：如果两个多边形不仅      ，而且对应顶点的连线            ，对应边       或                   ，那么这样的两个图形叫做位似图形，这个点叫做            ，这时的相似比又称为         ．

（2）掌握位似图形概念，需注意：

①位似是一种具有位置关系的相似，所以两个图形是位似图形，必定是    图形，而相似图形不一定是         图形；

②两个位似图形的位似中心只有一个；

③两个位似图形可能位于位似中心的两侧，也可能位于位似中心的一侧；

④位似比就是相似比．利用位似图形的定义可判断两个图形是否位似．

（3）位似图形上任意一对对应点到位似中心的距离等于              ．

（4）两个位似图形的主要特征是：每对位似对应点与位似中心共线；不经过位似中心的对应线段平行．

二、合作探究（课堂导学）

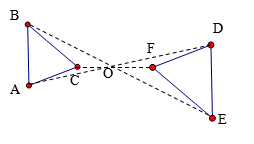
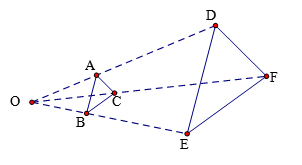实验探究1：如图，点O是△ABC外的一点，分别在射线OA、OB、OC上取一点D、E、F，使得,连接DE、EF、FD，所得△DEF与△ABC是否相似？证明你的结论。

 

 

 

 

 

 

 

 

 

 

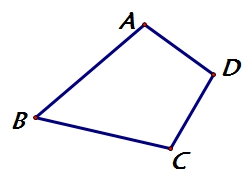
实验探究2：把图中的四边形ABCD缩小到原来的．

    分析：把原图形缩小到原来的，也就是使新图形上各顶点到位似中心的距离与原图形各对应顶点到位似中心的距离之比为1∶2 ．

 

作图时要注意:

1、首先确定位似中心，位似中心的位置可随意选择；

2、确定原图形的关键点，如四边形有四个关键点，即它的四个顶点；

3、确定位似比，根据位似比的取值，可以判断是将一个图形放大还是缩小；

4、符合要求的图形不惟一，因为所作的图形与所确定的位似中心的位置有关，

  并且同一个位似中心的两侧各有一个符合要求的图形

三、讨论交流（展示点评）

四、课堂检测（当堂训练）

1、如图，以O为位似中心，将放大为原来的两倍。

 

 

 

 

 

 

2．画出所给图中的位似中心．

 

 

 

拓展延伸（课外练习）：

1、四边形ABCD和四边形A1B1C1D1是位似图形，位似中心是点O，则它们的对应点的连线一定经过____________。

2、四边形ABCD和四边形A1B1C1D1是位似图形，点O是位似中心。如果OA：OA1=1:3，那么AB：A1B1=____________

3、如果四边形ABCD与四边形EFGH是位似图形，且位似比为,下列说法正确的是________。①△ABC∽△EFG  ②③。

4、如果正五边形FGHMN是由正五边形ABCDE经过位似变换得到的，若AB：FG=2：3，则下列结论正确的是(      )   

   A、2DE=3MN    B、3DE=2MN    C、3∠A=2∠F    D、2∠A=3∠F

5、用作位似图形的方法，可以将一个图形放大或缩小，位似中心位置可选在(    )

A、原图形的外部   B、原图形的内部  C、原图形的边上  D、任意位置

6、如图，△ABC与是位似图形，位似比为2：3，已知AB=4，则DE的长等于(      )

A、6    B、5    C、9    D、

 

 

 

 

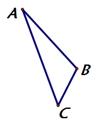
7．已知：如图，△ABC，画，使∽△ABC，且使相似比为1.5，要求

（1）位似中心在△ABC的外部；

（2）位似中心在△ABC的内部；

（3）位似中心在△ABC的一条边上；

（4）以点C为位似中心．