| 上传:admin | 审核发布:admin | 更新时间:2015-3-29 9:47:06 | 点击次数:716次 |
四川省米易中学校高中数学(新课标人教A版 必修二):2.1 空间点、直线、平面之间的位置关系教案
自主探究学习
能够从日常生活实例中抽象出数学中所说的“平面”;理解平面的无限延展性;正确地用图形和符号表示点、直线、平面以及它们之间的关系;初步掌握文字语言、图形语言与符号语言三种语言之间的转化;理解可以作为推理依据的三条公理.
1.平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC、平面ABCD等.
2.如果几个平面画在一起,当一个平面的一部分被另一个平面遮住时,应画成虚线或不画(打出投影片)
3.公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内
4.公理2:过不在一条直线上的三点,有且只有一个平面.
5.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
6. 公理2的三条推论:
①推论1 经过一条直线和这条直线外的一点,有且只有一个平面;
②推论2 经过两条相交直线,有且只有一个平面;
③推论3 经过两条平行直线,有且只有一个平面.
名师要点解析
要点导学
1. 点![]() 在直线上,记作
在直线上,记作![]() ;点
;点![]() 在平面
在平面![]() 内,记作
内,记作![]() ;直线
;直线![]() 在平面
在平面![]() 内,记作
内,记作![]() .
.
2. 平面基本性质即三条公理的“文字语言”、“符号语言”、“图形语言”列表如下:
|
|
公理1 |
公理2 |
公理3 |
|
图形语言 |
|
|
|
|
文字语言 |
如果一条直线上的两点在一个平面内,那么这条直线在此平面内. |
过不在一条直线上的三点,有且只有一个平面. |
如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. |
|
符号语言 |
|
|
|
3.公里的作用
(1)公理1作用:判断直线是否在平面内;
(2)公理2作用:确定一个平面的依据;
(3)公理3作用:判定两个平面是否相交的依据.
【经典例题】
【例】在正方体![]() 中.(1)
中.(1)![]() 与
与![]() 是否在同一平面内?(2)点
是否在同一平面内?(2)点![]() 是否在同一平面内?(3)画出平面
是否在同一平面内?(3)画出平面![]() 与平面
与平面![]() 的交线,平面
的交线,平面![]() 与平面
与平面![]() 的交线.
的交线.
【分析】利用公理1、公理2、公理3及公理2的推论来判定.
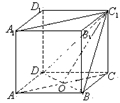 【解】(1)在正方体
【解】(1)在正方体![]() 中,
中,
∵![]() , ∴由公理2的推论可知,
, ∴由公理2的推论可知,![]() 与
与![]() 可确定平面
可确定平面![]() ,
,
∴![]() 与
与![]() 在同一平面内.
在同一平面内.
(2)∵点![]() 不共线,由公理3可知,点
不共线,由公理3可知,点![]() 可确定平面
可确定平面![]() ,
,
∴ 点![]() 在同一平面内.
在同一平面内.
(3)∵![]() ,
,![]() , ∴点
, ∴点![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴ 平面![]() 平面
平面![]()
![]() ,
,
同理平面![]() 平面
平面![]()
【点拨】确定平面的依据有公理2(不在同一条直线上的三点)和3个推论(两条平行直线、两条相交直线、直线和直线外一点). 对公理及推论的作用,应清楚明白.
2.1.2 空间中直线与直线之间的位置关系
自主探究学习
了解空间两条直线的三种位置关系,理解异面直线的定义,掌握平行公理,掌握等角定理,掌握两条异面直线所成角的定义及垂直.
1.两条直线的三种位置关系
(1)相交直线:同一平面内,有且只有一个公共点;
(2)平行直线:同一平面内,没有公共点;
(3)异面直线: 不同在任何一个平面内,没有公共点.
2. 公理4:平行于同一条直线的两条直线互相平行.
3. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等![]()
名师要点解析
要点导学
1. 空间两条直线的位置关系:
2. 已知两条异面直线![]() ,经过空间任一点
,经过空间任一点![]() 作直线
作直线![]() ,把
,把![]() 所成的锐角(或直角)叫异面直线
所成的锐角(或直角)叫异面直线![]() 所成的角(或夹角).
所成的角(或夹角). ![]() 所成的角的大小与点
所成的角的大小与点![]() 的选择无关,为了简便,点
的选择无关,为了简便,点![]() 通常取在异面直线的一条上;异面直线所成的角的范围为
通常取在异面直线的一条上;异面直线所成的角的范围为![]() ,如果两条异面直线所成的角是直角,则叫两条异面直线垂直,记作
,如果两条异面直线所成的角是直角,则叫两条异面直线垂直,记作![]() . 求两条异面直线所成角的步骤可以归纳为四步:选点→平移→定角→计算.
. 求两条异面直线所成角的步骤可以归纳为四步:选点→平移→定角→计算.
3. 公理4作用:判断空间两条直线平行的依据.
【经典例题】
【例1】判断下列命题的真假,真的打“√”,假的打“×”
(1)平行于同一直线的两条直线平行 ( )
(2)垂直于同一直线的两条直线平行 ( )
(3)过直线外一点,有且只有一条直线与已知直线平行 ( )
(4)与已知直线平行且距离等于定长的直线只有两条 ( )
(5)若一个角的两边分别与另一个角的两边平行,那么这两个角相等 ( )
(6)若两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等 ( )
【分析】依据公理4、异面直线所成角的定义及等角定理进行判断.
【解】(1)( √ );(2)( × );(3)( √ );(4)( × );(5)( × );(6)( √ ).
【点拨】注意在空间中思考问题,如问题(4),与已知直线平行且距离等于定长的直线在一个平面内是只有两条,但在空间中就有无数条.
【例】如图中,正方体ABCD—A1B1C1D1,E,F分别是AD,AA1的中点.
(1)求直线AB1和CC1所成的角的大小;
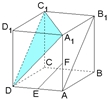 (2)求直线AB1和EF所成的角的大小.
(2)求直线AB1和EF所成的角的大小.
【分析】依据异面直线所成角的定义,借助正方体本身的性质,
依照选点、平移、定角、计算的步骤进行解答.
∴ DC1 和CC1所成的锐角∠CC1D就是AB1和CC1所成的角.
∵ ∠CC1D=45°, ∴ AB1 和CC1所成的角是45°.
(2)如图,连接DA1,A1C1,
∵ EF∥A1D,AB1∥DC1,∴ ∠A1DC1是直线AB1和EF所成的角.
∵ΔA1DC1是等边三角形, ∴ ∠A1DC1=60º,即直线AB1和EF所成的角是60º.
【点拨】求解异面直线所成角时,需紧扣概念,结合平移的思想,发挥空间想象力,把两异面直线成角问题转化为与两相交直线所成角,即将异面问题转化为共面问题,运用化归思想将陌生问题熟悉化.
2.1.3 空间中直线与平面之间的位置关系
2.1.4 平面与平面之间的位置关系
自主探究学习
了解直线与平面的三种位置关系,理解直线在平面外的概念,了解平面与平面的两种位置关系.
1.直线与平面有三种位置关系:
![]() (1)直线在平面内 —— 有无数个公共点
(1)直线在平面内 —— 有无数个公共点
(2)直线与平面相交 —— 有且只有一个公共点
(3)直线在平面平行 —— 没有公共点
2. 两个平面之间有两种位置关系:
(1)两个平面平行 —— 没有公共点
(2)两个平面相交 —— 有且只有一条公共直线
名师要点解析
要点导学
1. 直线与平面的位置关系:(1)直线在平面内(有无数个公共点);(2)直线与平面相交(有且只有一个公共点);(3)直线与平面平行(没有公共点). 分别记作:![]() ;
;![]() ;
;![]() .
.
2. 两平面的位置关系:平行(没有公共点);相交(有一条公共直线).分别记作![]() ;
;![]() .
.
【经典例题】
【例1】a//b且a与平面a相交,那么直线b与平面a的位置关系是( )
A.必相交 B.有可能平行
 C.相交或平行 D.相交或在平面内
C.相交或平行 D.相交或在平面内
【分析】可借助手边的模型进行判定.
【解】A
【点拨】解题时利用手边的模型或教室中的长方体模型可快速解决问题.
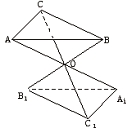
【例2】如![]() 右图,设△ABC和△A1B1C1的三对对应顶点的连线AA1,BB1,CC1相交于一点O,且
右图,设△ABC和△A1B1C1的三对对应顶点的连线AA1,BB1,CC1相交于一点O,且![]() =
=![]() =
=![]() =
= ![]() .试求
.试求![]() 的值.
的值.
【分析】利用相似三角形面积的比等于相似比的平方进行计算.
【解】依题意,因为AA1,BB1,CC1相交于一点O,且![]() =
=![]() =
=![]() ,
,
所以AB∥A1B1,AC∥A1C1,BC∥B1C1.
由平移角定理得∠BAC=∠B1A1C1,∠ABC=∠A1B1C1,△ABC∽△A1B1C1,
所以![]() =(
=(![]() )2=
)2=![]() .
.
【点拨】利用平移角定理,可证明空间两个角相等或两个三角形相似、全等;利用平行公理,可证明空间两条直线平行,从而解决相关问题.
2.2 直线、平面平行的判定及其性质
2.2.1 直线与平面平行的判定
自主探究学习
以立体几何的定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行的判定,理解直线与平面平行判定定理,初步掌握转化思想“线线平行![]() 线面平行”.
线面平行”.
直线与平面平行的判定定理:平面外一条直线与此平面![]() 内的一条直线平行,则该直线与此平面平行.
内的一条直线平行,则该直线与此平面平行.
简记为:线线平行,则线面平行
名师要点解析
要点导学
1.判定定理的符号表示为:![]() .
.
2. 证明线面平行的根本问题是要在平面内找一直线与已知直线平行,此时常用![]() 中位线定理、成比例线段、射影法、平行移动、补形等方法,具体用何种方法要视条件而定.
中位线定理、成比例线段、射影法、平行移动、补形等方法,具体用何种方法要视条件而定.
【经典例题】
【例1】如果平面a外有两点A,B,它们到平面a的距离都是a,则直线AB和平面a的位置关系一定是 ( )
A.平行 B.相交 C.平行或相交 D.ABÌa
【分析】a外有两点A,B,它们到平面a的距离都是a,并不能说明直线AB一定与a平行,因为两点A,B有可能在平面a的异侧.
【解】C
【点拨】思考问题时,思维要发散,不能定向思维.
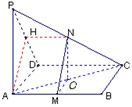 【例2】如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点
【例2】如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点![]()
(1)求证:MN//平面PAD;
(2)若![]() ,
,![]() ,求异面直线PA与MN所成的角的大小.
,求异面直线PA与MN所成的角的大小.
【分析】利用中位线或平行四边形找平行线,再利用线面平行的判定定理.
【解】(1)取PD的中点H,连接AH,由N是PC的中点,
∴ NH![]()
![]() . 由M是AB的中点, ∴ NH
. 由M是AB的中点, ∴ NH![]() AM,
AM,
即AMNH为平行四边形.
∴ ![]() .
.
由![]() , ∴
, ∴ ![]() .
.
(2) 连接AC并取其中点为O,连接OM,ON,
∴ OM![]()
![]() BC,ON
BC,ON![]()
![]() PA,
PA,
所以![]() 就是异面直线PA与MN所成的角,且MO⊥NO.
就是异面直线PA与MN所成的角,且MO⊥NO.
由![]() ,
,![]() , 得OM=2,ON=
, 得OM=2,ON=![]()
![]()
所以![]() ,即异面直线PA与MN成30°的角
,即异面直线PA与MN成30°的角![]()
【点拨】已知中点,牢牢抓住中位线得到线线平行,或通过找平行四边形得到线线平行,再通过线线平行转化为线面平行. 求两条异面直线所成角,方法的关键也是平移其中一条或者两条直线,得到相交的线线角,通过解三角形而得.
2.2.2 平面与平面平行的判定
自主探究学习
以立体几何的定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中面面平行的判定,理解两个平面平行的判定定理与应用及转化的思想.
一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
名师要点解析
要点导学
1.面面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.用符号表示为:![]() .
.
2. 垂直于同一条直线的两个平面平行.
3. 平面α上有不在同一直线上的三点到平面β的距离相等,则α与β的位置关系是平行或相交.
【经典例题】
【例1】判断下列命题的真假,真的打“√”,假的打“×”
(1)平面![]() 内有一条直线与平面
内有一条直线与平面![]() 平行,则
平行,则![]() 与
与![]() 平行 ( )
平行 ( )
(2)平面![]() 内有两条直线与平面
内有两条直线与平面![]() 平行,则
平行,则![]() 与
与![]() 平行 ( )
平行 ( )
(3)平面![]() 内有无数条直线与平面
内有无数条直线与平面![]() 平行,则
平行,则![]() 与
与![]() 平行 ( )
平行 ( )
(4)平面![]() 内有两条平行直线与平面
内有两条平行直线与平面![]() 平行,则
平行,则![]() 与
与![]() 平行 ( )
平行 ( )
(5)平面![]() 内任一条直线与平面
内任一条直线与平面![]() 平行,则
平行,则![]() 与
与![]() 平行 ( )
平行 ( )
【分析】依据面面平行的定义与判定定理进行判断.
【解】(![]() 1)( × );(2)( × );(3)( × );(4)( × );(5)( √ ).
1)( × );(2)( × );(3)( × );(4)( × );(5)( √ ).
【点拨】可借助于教室中的长方体模型进行面面平行的判断.
【例2】已知四棱锥P-ABCD中, 底面ABCD为平行四边形. 点M、N、Q分别在PA、BD、PD上, 且PM:MA=BN:ND=PQ:QD.求证:平面MNQ∥平面PBC.
【分析】利用平面与平面平行的判定定理进行证明,可寻找满足定理的5个条件.
【证明】![]() PM:MA=BN:ND=PQ:QD.
PM:MA=BN:ND=PQ:QD.
∴ MQ//AD,NQ//BP,
而BP![]() 平面PBC,NQ
平面PBC,NQ ![]() 平面PBC, ∴ NQ//平面PBC.
平面PBC, ∴ NQ//平面PBC.
又![]() ABCD为平行四边形,BC//AD, ∴ MQ//BC,
ABCD为平行四边形,BC//AD, ∴ MQ//BC,
而BC![]() 平面PBC,MQ
平面PBC,MQ ![]() 平面PBC, ∴ MQ//平面PBC.
平面PBC, ∴ MQ//平面PBC.
由MQ![]() NQ=Q,根据平面与平面平行的判定定理,
NQ=Q,根据平面与平面平行的判定定理,
∴ 平面MNQ∥平面PBC.
【点拨】由比例线段得到线线平行,依据线面平行的判定定理得到线面平行,证得两条相交直线平行于一个平面后,转化为面面平行. 一般证“面面平面”问题最终转化为证线与线的平行.
2.2.3 直线与平面平行的性质
自主探究学习
通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行的性质,掌握直线和平面平行的性质定理,灵活运用线面平行的判定定理和性质定理,掌握“线线”“线面”平行的转化.
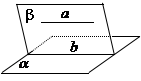 线面
线面![]() 平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.![]() 即:
即: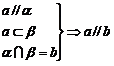 .
.
名师要点解析
要点导学
1. 如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
2. 直线和平面平行的判定定理及性质定理在解题时往往交替使用![]() .证线面平行往往转化为证线线平行,而证线线平行又将转化为证线面平行.循环往复直至证得结论为止.
.证线面平行往往转化为证线线平行,而证线线平行又将转化为证线面平行.循环往复直至证得结论为止.
【经典例题】
【例1】 (1)直线![]() ,
,![]() ,则
,则![]() 与平面
与平面![]() 的位置关系是_____________.
的位置关系是_____________.
(2)![]() 是两异面直线
是两异面直线![]() ,
,![]() 外的一点,过
外的一点,过![]() 最多可作___________个平面同时与
最多可作___________个平面同时与![]() ,
,![]() 平行.
平行.
【分析】(1)当直线![]() 在平面
在平面![]() 外时,
外时,![]() ;当直线
;当直线![]() 在平面
在平面![]() 内时,
内时,![]() . (2)因为过
. (2)因为过![]() 点分别作
点分别作![]() ,
,![]() 的平行线只能作一条,(分别称
的平行线只能作一条,(分别称![]() ,
,![]() )经过
)经过![]() ,
,![]() 的平面也是惟一的.所以只能作一个平面;还有不能作的可能,当这个平面经过
的平面也是惟一的.所以只能作一个平面;还有不能作的可能,当这个平面经过![]() 或
或![]() 时,这个平面就不满足条件了.
时,这个平面就不满足条件了.
【解】(1)![]() 或
或![]() .(2)1.
.(2)1.
【点拨】考虑问题要全面,各种可能性都要想到,是解答本题的关键.
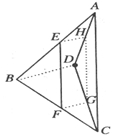
【例2】如右图,平行四边形EFGH的分别在空间四边形ABCD各边上,求证:BD//平面EFGH.
【分析】欲证![]() 平面EFGH,须证
平面EFGH,须证![]() 平行于平面内一条直线,显然,只要证
平行于平面内一条直线,显然,只要证![]() 即可.
即可.
 【证明】∵
【证明】∵ ![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴ ![]() .
.
又 ∵ ![]() ,
,![]() ,
,
∴ ![]() .
.
又 ∵ ![]() ,
,![]() ,
,
∴ ![]() .
.
【点拨】证明线面平行的转化思维链是“由已知线线平行→线面平行→线线平行→线面平行”.
2.2.4 平面与平面平行的性质
自主探究学习
通过直观感知、操作确认、思辨论证,认识和理解空间中面面平行的性质,掌握面面平行的性质定理,灵活运用面面平行的判定定理和性质定理,掌握“线线”“线面”“面面”平行的转化.
名师要点解析
要点导学
1. 面面平行的![]() 性质:如果两个平行
性质:如果两个平行![]() 平面同时与第三个平面相交,那么它们的交线平行. 用符号语言表示为:
平面同时与第三个平面相交,那么它们的交线平行. 用符号语言表示为:![]() .
.
2. 其它性质:
①![]() ;
;
②![]() ;
;
③夹在平行平面间的平行线段相等.
 【经典例题】
【经典例题】
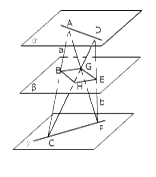
【例1】已知三个平面α,β,γ,α∥β∥γ,a,b是异面直线,
a与α,β,γ分别交于A,B,C三点,b与α,β,γ分别交于D,E,F三点,连接AF交平面β于G,连接CD交平面β于H,则四边形BGEH必为__________.
【分析】由α∥β∥γ,a与AF相交于A有:BG![]() 面ACF,∴ BG∥CF,同理有:HE∥CF,∴BG∥HE.同理BH∥GE,∴ 四边形BGEH为平行四边形.
面ACF,∴ BG∥CF,同理有:HE∥CF,∴BG∥HE.同理BH∥GE,∴ 四边形BGEH为平行四边形.
【解】平行四边形
【点拨】面面平行的性质有三条,均应熟记.
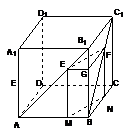 【例2】如图,已知正方体
【例2】如图,已知正方体![]() 中,面对角线
中,面对角线![]() ,
,![]() 上分别有两点E、F,且
上分别有两点E、F,且![]() . 求证:EF∥平面ABCD.
. 求证:EF∥平面ABCD.
【分析】证明线面平行的根本问题是要在平面内找一直线与已知直线平行,此时常用中位线定理、成比例线段、射影法、平行移动、补形等方法,本题可以用平行四边形找平行线,也可以用面面平行的性质定理.
【证明】证法一:过E,F分别作AB,BC的垂线,EM,FN分别交AB,BC于M,N,连接MN.
∵ BB1⊥平面ABCD, ∴BB1⊥AB,BB1⊥BC,∴ EM∥BB1,FN∥BB1, ∴EM∥FN,
∵ AB1=BC1,B1E=C1F,∴AE=BF, 又∠B1AB=∠C1BC=45°,
∴ Rt△AME≌Rt△BNF,∴EM=FN.
∴ 四边形MNFE是平行四边形,∴EF∥MN.
又MN![]() 平面ABCD,∴EF∥平面ABCD.
平面ABCD,∴EF∥平面ABCD.
证法二:过E作EG∥AB交BB1于G,连接GF,
∴![]() ,
,![]() ,
,![]() ,∴
,∴![]() , ∴FG∥B1C1∥BC.
, ∴FG∥B1C1∥BC.
又∵EG![]()
![]() =G,AB
=G,AB![]() BC=B,∴平面EFG∥平面ABCD.
BC=B,∴平面EFG∥平面ABCD.
b又EF![]() 平面EFG,∴EF∥平面ABCD.
平面EFG,∴EF∥平面ABCD.
【点拨】在熟知线面平行、面面平行的判定与性质之后,空间平行问题的证明,紧紧抓住“线线平行![]() 线面平行
线面平行![]() 面面平行”之间的互相转化而完成证明.
面面平行”之间的互相转化而完成证明.
2.3 直线、平面垂直的判定及其性质
2.3.1 直线与平面垂直的判定
自主探究学习
以立体几何的定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面垂直的判定,掌握直线与平面垂直的定义,理解直线与平面垂直的判定定理,并会用定义和判定定理证明直线与平面垂直的关系. 掌握线面角的定义及求解.
1.如果直线![]() 与平面
与平面![]() 内的任意一条直线都垂直,则直线
内的任意一条直线都垂直,则直线![]() 与平面
与平面![]() 互相垂直,记作
互相垂直,记作![]() .
. ![]() 是平面
是平面![]() 的垂线,
的垂线,![]() 是直线
是直线![]() 的垂面,它们的唯一公共点
的垂面,它们的唯一公共点![]() 叫做垂足.
叫做垂足.
2. 直线与平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,则这条直线与该平面垂直. 符号语言表示为:若![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∩
∩![]() =B,
=B,![]() Ì
Ì![]() ,
,![]() Ì
Ì![]() ,则
,则![]() ⊥
⊥![]()
名师要点解析
要点导学
1. 斜线和平面所成的角,简称“线面角”,它是平面的斜线和它在平面内的射影的夹角. 求直线和平面所成的角,几何法一般先定斜足,再作垂线找射影,然后通过解直角三角形求解,可以简述为“作(作出线面角)→证(证所作为所求)→求(解直角三角形)”. 通常,通过斜线上某个特殊点作出平面的垂线段,垂足和斜足的连线是产生线面角的关键.
2. 斜线和平面所成的角的范围是![]() .
.
【经典例题】
【例1】三棱锥![]() 中,
中,![]() ,
,![]() 平面ABC,垂足为O,求证:O为底面△ABC的垂心.
平面ABC,垂足为O,求证:O为底面△ABC的垂心.
【分析】可证O为三角形ABC的两条高线的交点.
【证明】连接OA、OB、OC,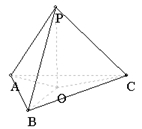 ∵
∵ ![]() 平面ABC,
平面ABC,
∴ ![]() .
.
又 ∵ ![]() ,
,
∴ ![]() ,得
,得![]() ,
,
∴ O为底面△ABC的垂心.
【点拨】此例可以变式为“已知![]() ,求证
,求证![]() ”,其思路是接着利用射影是垂心的结论得到
”,其思路是接着利用射影是垂心的结论得到![]() 后进行证明. 三条侧棱两两垂直时,也可按同样的思路证出.
后进行证明. 三条侧棱两两垂直时,也可按同样的思路证出.
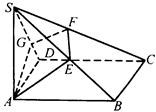 【例2】如图,
【例2】如图,![]() 是正方形,
是正方形,![]() 垂直于平面
垂直于平面![]() ,过
,过![]() 且垂直于
且垂直于![]() 的平面交
的平面交![]() 、
、![]() 、
、![]() 分别于点
分别于点![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() ,
,![]() .
.
【分析】本题考查线面垂直的判定与性质定理,
以及线线垂直和线面垂直相互转化的思想.由于
图形的对称性,所以两个结论只需证一个即可.
欲证![]() ,可证
,可证![]() 平面
平面![]() ,为此须
,为此须
证![]() ,
,![]() ,进而转化证明
,进而转化证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
【证明】∵![]()
![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,
∴![]() .
.
又∵![]() 为正方形,
为正方形,
∴![]() .
.
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,
∴![]() .
.
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,
∴![]() ,同理可证
,同理可证![]() .
.
【点拨】 (1)证明线线垂直,常用的方法有:同一平面内线线垂直、线面垂直的性质定理,三垂线定理与它的逆定理,以及与两条平行线中一条垂直就与另一条垂直.(2)本题的证明过程中反复交替使用“线线垂直”与“线面垂直”的相互联系,充分体现了数学化思想的优越性.
2.3.2 平面与平面垂直的判定
自主探究学习
通过直观感知、操作确认、思辨论证,认识和理解空间中面面垂直的判定,正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念;理解平面与平面垂直的判定定理并会用判定定理证明平面与平面垂直的关系,会用所学知识求两平面所成的二面角的平面角的大小.
1. 定义:从一条直线出发的两个半平面所组成的图形叫二面角. 这条直线叫做二面角的棱,这两个半平面叫做二面角的面. 记作二面角![]() . (简记
. (简记![]() )
)
2. 二面角的平面角:在二面角![]() 的棱
的棱![]() 上任取一点
上任取一点![]() ,以点
,以点![]() 为垂足,在半平面
为垂足,在半平面![]() 内分别作垂直于棱
内分别作垂直于棱![]() 的射线
的射线![]() 和
和![]() ,则射线
,则射线![]() 和
和![]() 构成的
构成的![]() 叫做二面角的平面角.
叫做二面角的平面角.
3. 定义![]() :两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直. 记作
:两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直. 记作![]() .
.
4. 判定:一个平面过另一个平面的垂线,则这两个平面垂直.
名师要点解析
要点导学
1. 二面角![]() 的大小
的大小
(1)二面角![]() 的大小是用它的平面角来度量的,以点
的大小是用它的平面角来度量的,以点![]() 为垂足,在半平面
为垂足,在半平面![]() 内分别作垂直于棱
内分别作垂直于棱![]() 的射线
的射线![]() 和
和![]() ,在做二面角的平面角时,一定要有“OA⊥l” ,OB⊥l;∠AOB的大小与点O在l上位置无关.
,在做二面角的平面角时,一定要有“OA⊥l” ,OB⊥l;∠AOB的大小与点O在l上位置无关.
(2)当二面角的平面角是直角时,这两个平面互相垂直.
2. 自二面角内一点分别向两个面引垂线,它们所成的角与二两角的平面角互补.
【经典例题】
【例1】已知两条不同直线![]() ,
,![]() ,两个不同平面
,两个不同平面![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①若![]() 垂直于
垂直于![]() 内的两条相交直线,则
内的两条相交直线,则![]() ⊥
⊥![]() ;②若
;②若![]() ∥
∥![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线;
内的所有直线;
③若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ;④若
;④若![]()
![]()
![]() ,
,![]() ,则
,则![]() ⊥
⊥![]() ;
;
⑤若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
【分析】①若![]() 垂直于
垂直于![]() 内的两条相交直线,则
内的两条相交直线,则![]() ⊥
⊥![]() ,正确;②若
,正确;②若![]() ∥
∥![]() ,则
,则![]() 平行于
平行于![]() 内的所有直线,l与
内的所有直线,l与![]() 还有可能异面;③若
还有可能异面;③若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() ,
,![]() 与
与![]() 还有可能平行或不垂直的相交;④若
还有可能平行或不垂直的相交;④若![]()
![]()
![]() ,
,![]() ,则
,则![]() ⊥
⊥![]() ,正确;⑤若
,正确;⑤若![]()
![]()
![]() ,
,![]()
![]()
![]() 且
且![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ,m与l还有可能异面;
,m与l还有可能异面;
【解】①④
 【点拨】根据线面、面面平行与垂直的判定与性质进行判断.
【点拨】根据线面、面面平行与垂直的判定与性质进行判断.
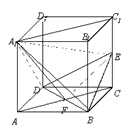
【例2】如图,在正方体![]() 中,E是
中,E是![]() 的中点,求证:
的中点,求证:![]() .
.
【分析】可证两个平面所成的二面角是直角.
【证明】连接AC,交BD于F,连接![]()
![]() ,EF,
,EF,![]() ,
,![]() .
.
由正方体![]() ,易得
,易得![]() ,
,![]() ,F是BD的中点, 所以
,F是BD的中点, 所以![]() ,得到
,得到![]() 是二面角
是二面角![]() 的平面角.
的平面角.
设正方体![]() 的棱长为2,则
的棱长为2,则
![]() ,
,![]() ,
,
![]() .
.
∴ ![]() ,即
,即![]() ,所以
,所以![]() .
.
【点拨】要证两平面垂直,证其二面角的平面角为直角,这也是证两平面垂直的常用方法. 此题由几何图形的特征,作出待证的两个垂直平面所成二面角的平面角是解决问题的关键.
2.3.3 直线与平面垂直的性质
自主探究学习
通过直观感知、操作确认、思辨论证,认识和理解空间中线面垂直的有关性质,掌握直线与平面垂直的性质定理;能运用性质定理解决一些简单问题;了解直线与平面垂直的判定定理和性质定理间的相互联系.
线面垂直性质定理:垂直于同一个平面的两条直线平行.
名师要点解析
要点导学
1.线面垂直性质定理的符号语言:![]()
2.如果两个平面都和一条直线垂直,那么这两个平面平行.
【经典例题】
【例1】三棱锥![]() 中,三个侧面与底面所成的二面角相等,
中,三个侧面与底面所成的二面角相等,![]() 平面ABC,垂足为O,求证:O为底面△ABC的内心.
平面ABC,垂足为O,求证:O为底面△ABC的内心.
【分析】可证点O到底面△ABC的三边的距离相等.
【证明】作![]() 于D,
于D,![]() 于E,
于E,![]() 于F,连接OD、OE、OF.
于F,连接OD、OE、OF.
∵ ![]() 平面ABC,∴
平面ABC,∴ ![]() ,
,![]() .
.
又 ∵ ![]() ,
,
∴ ![]() .
.
得 ![]() ,
,
∴![]()
![]() 为三个侧面与底面所成的二面角的平面角.
为三个侧面与底面所成的二面角的平面角. 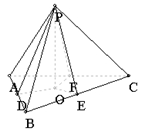
即得![]() ,
,
∵ PO边公共, ∴ ![]() ,得
,得 ![]() ,
,
又 ∵ ![]() .
.
∴ O为底面△ABC的内心.
【点拨】这里用到了证明垂直问题的转化思想,即“线线垂直→线面垂直→线线垂直”. 上述结论对于一般棱锥也成立,即棱锥的各侧面与底面所成二面角均相等,或棱锥的顶点到底面各边的距离相等,则顶点在底面上的射影为底面多边形的内切圆的圆心.
【例2】在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧棱
是正方形,侧棱![]() 平面
平面![]() .
.
(1)证明:![]() ;
;
(2)证明:![]() ;
;
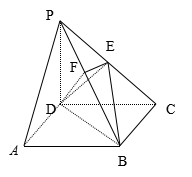 (3)求二面角
(3)求二面角![]() 的大小.
的大小.
【分析】(1)用线面平行的判定定理,在平面EDB中找与PA平行的直线;(2)用线面垂直的判定定理,在平面EFD中找与PB垂直的两条相交直线;(3)先依据二面角的定义找出二面角![]() 的平面角,再证明并求出来.
的平面角,再证明并求出来.
【解】(1)证明:连接![]() .
.
因为底面![]() 是正方形,所以
是正方形,所以![]() 的中点.
的中点.
在![]() 中,
中,![]() 是中位线,所以
是中位线,所以![]() .
.
而![]() ,
,
![]() .
.
(2)因为![]() ,
,
![]() ,
,
又![]() ,
,
![]() 是等腰直角三角形,而
是等腰直角三角形,而![]() 是斜边
是斜边![]() 的中线,
的中线,
![]() ①
①
同理可得![]() .
.
因为底面![]() 是正方形,有
是正方形,有![]() ,
,
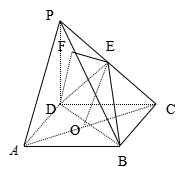
![]() .
.
而![]() ,
,
![]() ②
②
由①和②推得:![]() .
.
而![]() ,
,
![]() ,
,
又![]() ,
,
![]() .
.
(3)由(2)知![]() 的平面角.
的平面角.
由(2)知![]() .
.
设正方形![]() 的边长为
的边长为![]() ,
,
![]() ,
,
![]() ,
,
在![]() ,
,
在![]() ,
,
![]() .
.
【点拨】依据题目条件,寻找联系,实现平行关系、![]() 垂直关系、垂直与平行关系之间的转化.
垂直关系、垂直与平行关系之间的转化.
2.3.4 平面与平面垂直的性质
自主探究学习
理解平面与平面垂直的性质定理;能运用性质定理解决一些简单问题;了解面与平面垂直的判定定理和性质定理间的相互联系.
面面垂直性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
名师要点解析
要点导学
面面垂直性质定理用符号语言表示为:若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
【经典例题】
【例1】下面有4个命题:
①与同一个平面平行的两条![]() 直线平行; ②与同一条直线垂直的两条直线平行;
直线平行; ②与同一条直线垂直的两条直线平行;
③与同一个平面平行的两个平面平行; ④与同一个平面垂直的两个平面平行;
其中正确的命题有 【 】
A.4个 B.3个 C.2个 D.1个
【分析】①不正确,与同一个平面平行的两条直线还可能相交;②不正确,与同一条直线垂直的两条直线还可能异面;③正确,由平面平行的性质可知;④不正确,与同一个平面垂直的两个平面还有可能相交.
【解】D
【点拨】根据线面、面面平行与垂直的性质进行判定.
【例2】已知两个平面垂直,下列命题中正确的有 【 】
①一个平面内已知直线必垂直于另一个平面内的任意直线;
②一个平面内的已知直线必垂直于另一个平面内的无数条直线;
③一个平面内的任意一条直线必垂直于另一个平面;
④过一个平面内的任意一点做交线的垂线,则此垂线必垂直于另一个平面.
A. 3个 B.2个 C. 1 个 D .0个
【分析】①不正确;②正确;③不正确;④正确.
【解】B.
【点拨】根据线面、面面平行与垂直的性质进行判定.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

