| 上传:admin | 审核发布:admin | 更新时间:2015-3-29 11:08:45 | 点击次数:837次 |
直线的交点坐标与距离公式(强![]() 化训练)
化训练)
1. 已知集合M={(x,y![]() )∣x+y=2},N={(x,y)∣x–y=4},那么集
)∣x+y=2},N={(x,y)∣x–y=4},那么集![]() 合M∩N为( )
合M∩N为( )
A. {3,–1} ![]() B. 3,–1 C. (3,–1) D.{(3,–1)}
B. 3,–1 C. (3,–1) D.{(3,–1)}
答案:D
2. 如果直线y=ax+2与直线y=3x+b关于直线y=x对称,那么a,b的![]() 值分别是( )
值分别是( )
A.![]() ,6 B.
,6 B.![]() ,-6 C.3,-2
,-6 C.3,-2 ![]() D.3,6
D.3,6
答案:A
3. 已知直线y=kx+2k+1与直线y=–![]() x+2的交点位于第一象限,则实数k的取值范围
x+2的交点位于第一象限,则实数k的取值范围![]() 是( )
是( )
A![]() .–6<k<2 B.–
.–6<k<2 B.–![]() <k<0
<k<0 ![]() C.–
C.–![]() <k<
<k<![]() D.
D.![]() <k<+∞
<k<+∞
答案:C
4. 已![]() 知M(5cos
知M(5cos![]() ,5sin
,5sin![]() ),N(4cos
),N(4cos![]() ,4 sin
,4 sin![]() ), 则|MN|的
), 则|MN|的![]() 最大值( )
最大值( )
A. 9 B. 7 C. ![]() 5 D. 3
5 D. 3
答案:A
5、 证明平行四边行四条边的平方和等于两条对角线的平方和。
分析![]() :首先要建立直角坐标系,用坐标表示有关量
:首先要建立直角坐标系,用坐标表示有关量![]() ,然后用代数进行运算,最后把代数运算“翻译”成几何关系。
,然后用代数进行运算,最后把代数运算“翻译”成几何关系。
这一道题可以让学生讨论解决,让学生深刻体会数形之间的关系和转化,并从中归纳出应用代数![]() 问题解决几何问题的基本步骤。
问题解决几何问题的基本步骤。
![]() 证明:如图所示,以顶点A为坐标原点,AB边所在的直线为x轴,建立直角坐
证明:如图所示,以顶点A为坐标原点,AB边所在的直线为x轴,建立直角坐![]() 标系,有A(0,0)。
标系,有A(0,0)。
设B(a,0),D(b,c),由平行四边形的性质的点C的坐标为(a+b,c),因为
![]()
![]()
![]()
![]()
![]()
所以,![]()
![]()
![]()
![]() 所以,
所以,
![]()
因此,平行四边形四条边的平![]() 方和等于两条对角线的平方和。
方和等于两条对角线的平方和。
6、已知两条平行线直线![]()
![]() 和
和![]() 的
的![]() 一般式方程
一般式方程![]() 为
为![]() :
:![]() ,
,
![]() :
:![]() ,则
,则![]() 与
与![]() 的距
的距![]() 离为
离为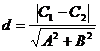
![]()
证明:设![]() 是直线
是直线![]() 上任一点,则点P0到直线
上任一点,则点P0到直线![]() 的距离为
的距离为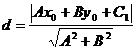
![]()
![]() 又
又 ![]()
即![]() ,∴
,∴![]() d=
d=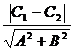
![]()
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

