| 上传:admin | 审核发布:admin | 更新时间:2015-3-30 10:44:24 | 点击次数:796次 |
河北省石家庄市第一中学高中数学 2.3 等差数列的前n项和教案 新人教A版必修5

教学过程:
一、导入新课
1.讲述高斯求1到100之和的故事.
2.问题:请同学们回答高斯算法的思路依据.
3.问题:1到100这100个数恰好是正整数这个等差数列的前100项,那么这种求和的方法是否具有普遍性?对一般的等差数列是否都可以按此方法求其前![]() 项的和呢?
项的和呢?
二、讲授新课
1.推导等差数列的前![]() 项和公式(倒序求和法):
项和公式(倒序求和法):
(1)定义:![]()
(2)公式:![]()
![]()
相加,![]()
∵ ![]() , ∴
, ∴ ![]()
∴ ![]() 知道首项、末项和项数,即可求
知道首项、末项和项数,即可求![]() .
.
又![]() ,
,
∴ ![]() 知道首项、公差和项数,即可求
知道首项、公差和项数,即可求![]() .
.
2.公式:
公式一:![]() .
.
公式二:![]() .
.
说明:
(1)注意以上公式是表示从等差数列第一项起至第![]() 项的连续有限项的和,其实对于等差数列的任意项起的连续有限项的和都可以用以上公式求,只是注意首项和项数的变化.
项的连续有限项的和,其实对于等差数列的任意项起的连续有限项的和都可以用以上公式求,只是注意首项和项数的变化.
(2)公式一反映的是等差数列中项与项的关系;公式二反映的是等差数列中项数与项的函数关系,显然前![]() 项和是项数
项和是项数![]() 的没有常数项的二次函数,即
的没有常数项的二次函数,即
![]() .
.
(3)公式中各含有4个元素:![]() 与
与![]() ,已知其中3个量,即可求出另外1个;综合通项公式及前
,已知其中3个量,即可求出另外1个;综合通项公式及前![]() 项和公式,已知其中3个量即可求出另外2个量.
项和公式,已知其中3个量即可求出另外2个量.
(4)利用函数观点研究![]() :
:![]()
①当![]() 时,
时,![]() 为二次函数,且无常数项.
为二次函数,且无常数项.
②当![]() 时,
时,![]() 有最小值; 题型:求
有最小值; 题型:求![]() 的最值.
的最值.
③当![]() 时,
时,![]() 有最大值.
有最大值.
3.等差数列的前![]() 项和的性质:
项和的性质:
(1)![]() 仍成等差,且公差为
仍成等差,且公差为![]() ;
;
(2)若项数为![]() ,则
,则
①![]() 与
与![]() 中项数相等,且
中项数相等,且![]() ;
;
②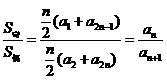 .
.
若项数为![]() ,则
,则
①![]()
![]()
![]() ;
;
②![]() ,
,![]() ;
;
③![]() ;
;
④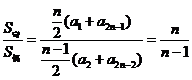 .
.
练习:已知项数为奇数的等差数列,![]() ,
,![]() ,求
,求![]() =11.
=11.
(3)![]() 等差(须证明) 应用见例7练习.
等差(须证明) 应用见例7练习.
4.应用举例:
(1)五个量知三求二
例1.课本P43 例1.
例2.课本P44 例2.
例3.等差数列![]() 中,
中,![]() ,求公差
,求公差![]() 和项数
和项数![]() .
.
解:选择公式 ![]() .
.
![]() , ∴
, ∴ ![]() ∴
∴ ![]() .
.
例4.课本P44 例3.
例5.课本P45 例4.
说明:由例5可以知道等差数列前![]() 项和是项数
项和是项数![]() 的没有常数项的二次函数,即
的没有常数项的二次函数,即![]() .进一步可以让学生研究如果一个数列的前
.进一步可以让学生研究如果一个数列的前![]() 项和公式是
项和公式是![]() ,那么这个数列是不是等差数列?如果不是,那么在什么情况下才是等差数列?
,那么这个数列是不是等差数列?如果不是,那么在什么情况下才是等差数列?
例6.(1)已知在等差数列![]() 中,
中,![]() ,求:
,求:![]() 的值.
的值.
解:∵ ![]() ,又∵
,又∵ ![]() ,
,
∴ ![]() .∴
.∴ ![]() .
.
(2)已知在等差数列![]() 中,
中,![]() ,求:
,求:![]() 的值.
的值.
解:∵ ![]() , ∴
, ∴ ![]() .
.
又∵ ![]() , ∴
, ∴ ![]() .
.
(3)已知数列![]() ,求其前
,求其前![]() 项和
项和![]() 的最小值.
的最小值.
解:由已知知此数列是等差数列,且![]() ,
,
∴ ![]() , ∴
, ∴ ![]() .
.
(2)证明等差数列问题
例7.求证:![]() 为等差数列
为等差数列![]() 其前n项和
其前n项和![]() .
.
证明:(![]() )已知
)已知![]() ,
,
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,且
,且![]() 符合上式.
符合上式.
∴ ![]() ,
,![]()
![]() (非零常数)
(非零常数)
∴ ![]() 为公差非零的等差数列.
为公差非零的等差数列.
(![]() )已知
)已知![]() 为公差非零的等差数列,不妨设首项为
为公差非零的等差数列,不妨设首项为![]() ,公差为
,公差为![]() .
.
则![]() ,令
,令![]() ,
,![]() ,
,
∴ ![]() .
.
综上可知,结论成立.
练习:证明:若数列![]() 为等差数列
为等差数列![]() 成等差.
成等差.
证明:∵ 数列![]() 为等差数列 ∴
为等差数列 ∴![]()
∴ ![]() ,
,
∴ ![]() ,得证.
,得证.
(3)综合问题
例8.等差数列![]() 中,
中,![]() 为前
为前![]() 项和,
项和,![]()
![]() ,问此数列前多少项的和最大?
,问此数列前多少项的和最大?
方法一:由![]() 即
即 ![]()
得![]() ,
,
且![]() ,∴
,∴![]() ,
,
又∵ ![]() 数列为减数列 ∴
数列为减数列 ∴ ![]()
∴ 当![]() 时,
时,![]() 最大,且
最大,且![]() .
.
方法二:(由![]() 为二次函数,对
为二次函数,对![]() 进行配方n取最接近对称轴的正整数时,
进行配方n取最接近对称轴的正整数时,![]() 最大.)
最大.)
由![]() 得
得 ![]() ∴
∴ ![]()
又 ![]() ,得
,得![]() .
.
∴ ![]()
∴ 当![]() 时,
时,![]() 最大,且
最大,且![]() .
.
方法三:同方法二,得![]()
∴ ![]() 令
令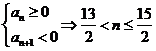
∵ ![]() ∴
∴ ![]() 时,
时,![]() 最大,且
最大,且![]() .
.
方法四:图象法 由![]() ,知对称轴为
,知对称轴为![]() .所以
.所以![]() 最大.
最大.
小结:
(I)等差数列的单调性的应用:
(1)当![]() 时,
时,![]() 有最大值,n是不等式
有最大值,n是不等式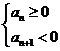 的正整数解时取得;
的正整数解时取得;
(2)当![]() 时,
时,![]() 有最大值,n是不等式
有最大值,n是不等式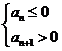 的正整数解时取得.
的正整数解时取得.
(II)当数列中有某项值为0时,![]() 应有两解.
应有两解.![]() .
.
例9.在等差数列![]() 中,
中,![]() .
.
(1)求公差![]() 的范围;
的范围;
(2)问![]() 中哪个值最大?
中哪个值最大?
解:
(1)由题意得 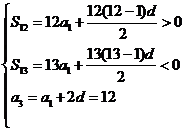 解之得,
解之得,![]() .
.
(2) ∵ ![]() ∴
∴ ![]() 为开口向下的二次函数.
为开口向下的二次函数.
方案1:利用函数求最值
![]()
对称轴为![]() ,∵
,∵![]() ∴
∴ ![]()
∴ ![]() 时,
时, ![]() 最大.
最大.
方案2:利用数列的单调性
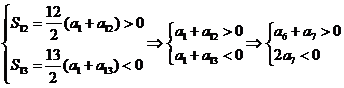
∴ ![]() ∴前6项和最大.
∴前6项和最大.
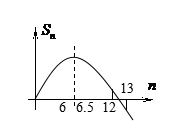 方案3:利用函数图象(适用于选择填空)
方案3:利用函数图象(适用于选择填空)
![]() 的根为0,
的根为0,![]() ,且
,且 ![]()
对称轴为![]()
6离对称轴较近,所以![]() 最大.
最大.
例10.等差数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 之比为
之比为![]()
![]() ,求
,求![]() 及
及![]() .
.
解:方法一: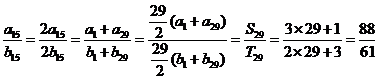
同理![]() .(只适用于上下角标相同的)
.(只适用于上下角标相同的)
方法二:设![]() (通法)
(通法)
![]() ,
,![]()
∴ ![]() ;
;![]() .
.
结论:等差数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() ,则
,则![]() .
.
变式:等差数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 之比为
之比为![]()
![]() ,求
,求![]() .
.
解:设![]() ,
,![]() ,
,
![]() ,
, ![]() .
.
上下角标不同时,![]() ,但是
,但是![]() .
.
例11.等差数列![]() 中,
中,![]() ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() .
.
解:由题意,得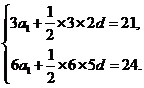 解得:
解得:![]() .
.
∴ ![]() .令
.令![]() ,得
,得![]() .
.
当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]()
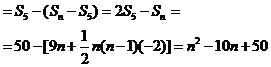
∴ 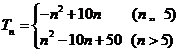
例12.(1)等差数列![]() 前
前![]() 项和为30,且前
项和为30,且前![]() 项和为100,求其前
项和为100,求其前![]() 项和.
项和.
(2)有一个项数为![]() 的等差数列,求它的奇数项之和与偶数项之和的比.
的等差数列,求它的奇数项之和与偶数项之和的比.
(3)等差数列![]() 前12项之和为354,其中奇数项之和与偶数项之和的比为27:32,求公差
前12项之和为354,其中奇数项之和与偶数项之和的比为27:32,求公差![]() .
.
(4)已知等差数列![]() ,
,![]() ,求
,求![]() .
.
(5)等差数列![]() 前
前![]() 项和为
项和为![]() ,
,![]() ,求
,求![]()
解:(1)30,100-30,![]() -100等差,所以,前
-100等差,所以,前![]() 项和为210.
项和为210.
另解:由![]() ,得
,得![]() ,即
,即![]() ,即可.
,即可.
(2)奇数项有![]() 个,偶数项
个,偶数项![]() 个.
个.
![]() ,所以
,所以 ![]() .
.
结论:在等差数列中,有![]() .
.
(3)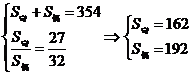 ,又
,又![]() .或用基本量计算.
.或用基本量计算.
(4)由已知得![]() ,利用
,利用![]() 或
或![]() .
.
(5)方法一:用基本量(整体代换)
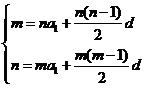 两式作差
两式作差
![]()
即 ![]() ,
,
![]()
方法二:利用![]() 等差,得
等差,得![]() 三点共线,斜率相等即可得到.
三点共线,斜率相等即可得到.
三、归纳总结
1.知识总结:
(1)本节介绍了一种求数列前![]() 项和的方法――倒序求和法.
项和的方法――倒序求和法.
(2)等差数列前![]() 项和公式:
项和公式:![]() ,
,![]() .
.
2.方法总结:
(1)要会根据公式列方程求等差数列的基本元素;
(2)学会灵活应用等差数列的性质解题;
(3)会应用函数思想研究数列问题.
四、作业及练习:
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

