二次函数 的图象和性质

知识点：1、二次函数的对称轴为         ，顶点坐标为          ，它的最高（低）点在    点，当       时，它有最大（小）值，值为          。

2、在抛物线中，为抛物线与        交点的纵坐标。

当时，图象开口       ，有最     点，且      时，随的增大而增大，

      时，随的增大而减小；

当时，图象开口       ，有最     点，且      时，随的增大而增大，

      时，随的增大而减小；

3、抛物线可由抛物线进行左（右）、上（下）平移得到。

一、选择题：

1、抛物线的顶点坐标为（   ）

A、（-2,3）         B、（2,11）         C、（-2,7）            D、（2，-3）

2、若抛物线与轴交于点（0，-3），则下列说法不正确的是（   ）

A、抛物线开口方向向上                 B、抛物线的对称轴是直线

C、当时，的最大值为-4          D、抛物线与轴的交点为（-1,0），（3,0）

3、要得到二次函数的图象，需将的图象（   ）

A、向左平移2个单位，再向下平移2个单位 B、向右平移2个单位，再向上平移2个单位

C、向左平移1个单位，再向上平移1个单位 D、向右平移1个单位，再向下平移1个单位

4、在平面直角坐标系中，若将抛物线先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后，所得到的抛物线的顶点坐标为（   ）

A、（-2,3）       B、（-1,4）       C、（1,4）        D、（4,3）

5、抛物线的图象向右平移2个单位，再向下平移3个单位，所得图象的解析式为，则、的值为（   ）

A、   B、  C、  D、

6、二次函数y=ax²+bx+1（a≠0）的图象的顶点在第一象限，且过点（-1，0）．设t=a+b+1，则t值的变化范围是（   ）

A．0＜t＜1     B．0＜t＜2     C．1＜t＜2     D．-1＜t＜1

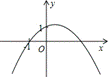
7、已知二次函数的图象如图所示对称轴为x=．下列结论中，正确的是（　　）

A．    B．    C．    D． 

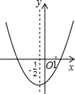
8、二次函数的图像如图所示，反比列函数与正比列函数在同一坐标系内的大致图像是（    ）

二、填空题：

1、抛物线的开口方向向     ，对称轴是          ，最高点的坐标是

         ，函数值得最大值是       。

2、抛物线变为的形式，则=       。

3、抛物线的最高点为（-1，-3），则            。

4、若二次函数的图象经过点（-1,0），（1，-2），当随的增大而增大时，的取值范围是             。

5、把抛物线先向右平移3个单位，再向下平移2个单位，所得抛物线解析式为，则=     。

6、在平面直角坐标系中，若将抛物线y=2x²-4x+3先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是            。

7、抛物线（）的对称轴为直线,且经过点（—1，），（2，）

则试比较与的大小：     （填“>”“<”或“=”）。

8、已知二次函数y=x²-7x+，若自变量x分别取x₁，x₂，x₃，且0＜x₁＜x₂＜x₃，则对应的函数值y₁，y₂，y₃的大小关系是             （用“<”连接）。

9、二次函数的图象关于原点O（0, 0）对称的图象的解析式是_________________。

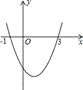
10、已知二次函数y=ax²+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0）．对于下列命题：①b-2a=0；②abc＜0；③a-2b+4c＜0；④8a+c＞0．其中正确的有                。

三、解答题：

1、已知抛物线的对称轴为，且经过点（1,4）和（5,0），试求该抛物线的表达式。