| 上传:吴小勇 | 审核发布:admin | 更新时间:2017-12-23 19:54:18 | 点击次数:535次 |
【湘教版】数学八年级上册:期末测试卷
(时间:90分钟 满分:120分)
一、选择题(每小题3分,共24分)
1.要使分式![]() 的值为0,你认为x可取的数是( )
的值为0,你认为x可取的数是( )
A.9 B.±3 C.-3 D.3
2.下列长度的三条线段不能组成三角形的是( )
A.1,2,3 B.3,4,5 C.4,5,6 D.6,8,10
3.下列各式属于最简二次根式的是( )
A.![]()
![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列各数中,3.141 59,-![]() ,0.131 13
,0.131 13![]() 1 113……,-π,
1 113……,-π,![]() ,-
,-![]() ,无理数的个数有( )
,无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
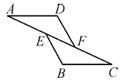
5.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC
6.下列各式![]() 计算正确的是( )
计算正确的是( )
A.![]() -2
-2![]() =-
=-![]() B.
B.![]() =4a(a>0)[来源:学科网ZXXK]
=4a(a>0)[来源:学科网ZXXK]
C.![]() =
=![]() ×
×![]()
![]() D.
D.![]() ÷
÷![]() =
=![]()
7.满足不等式组![]() 的整数m的值有( )
的整数m的值有( )
A.1个 B.2个 C.3个 D.4个
8.甲队修路120 m与乙队修路100 m所用天数相同,已知甲队比乙队每天多修10 m,设甲队每天修路x m.依题意,下面所列方程正确的是( )
A.![]() =
=![]() B.
B.![]() =
=![]() C.
C.![]() =
=![]() D.
D.![]() =
=![]()
二、填空题(每小题3分,共24分)
9.使式子![]() 有意义的x的取值范围是 .
有意义的x的取值范围是 .
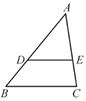
10.如图,△ABC中,点D,E分别在AB、AC边上,DE∥BC,∠A=50°,∠C=70°,那么∠ADE的度数是 .
11.25的平方根是 .
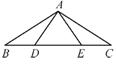
12.如图,点D,E在△ABC的BC边上,∠B=∠C,要推理得出△ABE≌△ACD,可以补充的一个条件是 .(不添加辅助线,写出一个即可)
13.若整数x满足|x|≤3,则使![]() 为整数的x的值是
为整数的x的值是 ![]() .(只需填一个)
.(只需填一个)
14.把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式: .
15.当k 时,方![]() 程4(
程4(![]() -k)+5=-2k的解不大于-3.
-k)+5=-2k的解不大于-3.
16.观察下面的一列二次根式,并填空.

第n个二次根式可表示为 .(用含n的代数式表示)
三、解答题(共72分)
17.(6分)解方程:![]() =
=![]() -1.
-1.
18.(6分)已知不等式:(1)2x-1>![]() x;(2)
x;(2)![]() <-1;(3)x+8<4x-1.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来.
<-1;(3)x+8<4x-1.你喜欢其中哪两个不等式,请把它们选出来组成一个不等式组,求出它的解集,并在数轴上把解集表示出来.
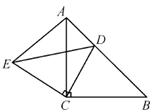
19.(6分)已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点.求证:BD=AE.
20.(8分)计算:
(1)-22-(-![]() )-2-|2-2
)-2-|2-2![]() |+
|+![]() ; (2)(2
; (2)(2![]() +
+![]() )(2
)(2![]() -
-![]() )-
)-![]() ·(
·(![]() -
-![]() ).
).
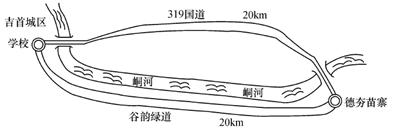
21.(8分)吉首城区某中学组织学生到距学校20 km的德夯苗寨参加社会实践活动,一部分学生沿“谷韵绿道”骑自行车先走,半小时后,其余学生沿319国道乘汽车前往,结果他们同时到达(两条道路路程相同),已知汽车速度是自行车速度的2倍,求骑自行车学生的速度.
22.(8分)某城市平均每天生产垃圾700吨,由甲、乙两个垃圾处理厂处理,已知甲厂每小时可处理垃圾55吨,需费用550元,乙厂每小时可处理垃圾45吨,需费用495元,若规定该城市每天处理垃圾的费用不超过7 370元,甲厂每天处理垃圾至![]() 少需要多少小时?
少需要多少小时?
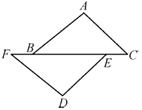
23.(10分![]() )如图,点F,B,E,C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
)如图,点F,B,E,C在同一直线上,并且BF=CE,∠ABC=∠DEF.能否由上面的已知条件证明△ABC≌△DEF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使△ABC≌△DEF,并给出证明.
提供的三个条件是:①AB=DE;②AC=DF;③![]() AC∥DF.
AC∥DF.
24.(10分)观察下列各式:![]() =
=![]() ;
;![]() =
=![]() ;
;![]() =
=![]() ;……
;……
(1)按上述两个等式的特征,请猜想![]() = ;
= ;
(2)针对上述各式反映的规律,写出用n(n为自然数且n≥2)表示的式子;
(3![]() )证明你在(2)中写的结论成立.
)证明你在(2)中写的结论成立.
25.(10分)2013年4月20日,雅安发生7.0级地震,某地需550顶帐篷解决受灾群众临时住宿问题,现由甲、乙两个工厂来加工生产.已知甲工厂每天的加工生产能力是乙工厂每天加工生产能力的1.5倍,并且加工生产240顶帐篷甲工厂比乙工厂少用4天.
(1)求甲、乙两个工厂每天分别可加工生产多少顶帐篷?
(2)若甲工厂每天的加工生产成本为3万元,乙工厂每天的加工生产成本为2.4万元,要使这批救灾帐篷的加工生产总成本不高于60万元,至少应安排甲工厂加工生产多少天?
参考答案
1.D 2.A 3.B 4.B 5.B 6.A 7.A 8.A
9.x≥-![]() 10.60° 11.±5 12.答案不唯一,如∠ADE=∠AED或BD=CE或BE=CD
10.60° 11.±5 12.答案不唯一,如∠ADE=∠AED或BD=CE或BE=CD
13.3或-2 14.如果两条直线垂直于同一条直线,那么这两条直线平行
15.≤-0.5 16.![]()
17.方程两边同乘以(x-2)(x+3),得6(x+3)=x(x-2)-(x-2)(x+3),
去括号,得6x+18=x2-2x-x2-x+6,
移项、合并同类项,得9x=-12,
系数化为1,得x=-![]() .
.
经检验,x=-![]() 是原方程的解.
是原方程的解.
所以原![]() 方程的解是x=-
方程的解是x=-![]() .[来源:Zxxk.Com]
.[来源:Zxxk.Com]
18.答案不唯一,写出其中一种即可.
第一组:由(![]() 1)和(2)得:
1)和(2)得: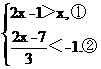
解①得x>1.解②得x<2.不等式组的解集为1<x<2.在数轴上表示解集略.
第二组:由(1)和(3)得: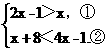
解①得x>1.解②得x>3.不等式组的解集为![]() x>3.在数轴上表示解集略.
x>3.在数轴上表示解集略.
第三组:由(2)和(3)得: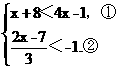
解①得x>3.解②得x<2.不等式组无解.在数轴上表示解集略.
19.证明:∵△ABC和△ECD都是等腰直角三角形,
∴CD=CE,AC=BC,∠ECD=∠ACB=90°.
∴∠ECD-∠ACD=∠ACB-∠ACD,即∠ACE=∠BCD.[来源:学科网ZXXK]
在△ACE与△BCD中,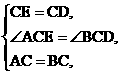
∴△ACE≌△BCD(SAS).∴BD=AE.
20.(1)原式=-6. (2)原式=![]() +2
+2![]() .
.
21.设骑自行车学生的速度为x km/h,则汽车的速度为2x km/h,根据题意得:
![]() -=
-=![]() .解得:x=20.
.解得:x=20.
经检验,x=20是原方程的解.
答:骑自行车学生的速度为20 km/h.
22.设甲厂每天处理垃圾x吨,则乙厂每天处理垃圾(700-x)吨,根据题意,得
![]() ×550+
×550+![]() ×495≤7 370.解得x≥330.[来源:学科网ZXXK]
×495≤7 370.解得x≥330.[来源:学科网ZXXK]
330÷55=6(小时).
答:甲厂每天处理垃圾至少需要6小时.
23.由前面的已知条件不能证明△ABC≌△DEF.需要再添加条件.
添加条件①时,证明:∵BF=CE,∴EF=BC,
∵∠ABC=∠DEF,AB=DE,∴△ABC≌△DEF(SAS).
添加条件③时,∵AC∥DF,∴∠ACB=∠DFE,
∵BF=CE,∴EF=BC,
又∠ABC=∠DEF,∴△ABC≌△DEF(ASA);
添加条件②AC=DF,此时是SSA不能证明全等.
24.(1)![]()
(2)n![]() =
=![]() .
.
(3)理由:n![]() =
=![]() =
=![]()
![]() =
=![]() =
=![]() ,故结论成立.
,故结论成立.
25.(1)设乙工厂每天加工生产x顶帐篷,甲工厂每天加工生产1.5x顶帐篷.根据题意,得
![]() +4=
+4=![]() .解得x=20.
.解得x=20.
经检验,x=20为原方程的根.
则1.5x=30.
答:乙工厂每天加工生产20顶帐篷,甲工厂每天加工生产30顶帐篷.[来源:学科网]
(2)设甲工厂生产m天,则
这批救灾帐篷的加工生产总成本:3m+2.4×![]() =-
=-![]() m+66,
m+66,
∴-![]() m+66≤60.解这个不等式得m≥10.
m+66≤60.解这个不等式得m≥10.
答:至少应安排甲工厂加工生产10天.
| 3.3_立方根.ppt | |
| 已经到最后一个 |
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

