| 上传:kisszhoushumei | 审核发布:admin | 更新时间:2015-6-4 14:57:04 | 点击次数:436次 |
1.2.2 函数的表示法
![]()
1.下列图形是函数y=-|x|(x∈[-2,2])的图象的是( )
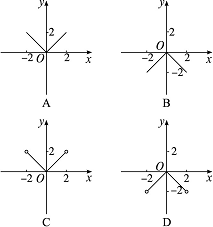
2.给出下列四个对应,其中构成映射的是…( )
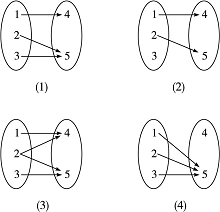
A.(1)(2) B.(1)(4)
C.(1)(3)(4) D.(3)(4)
3.函数y=的值域为( )
A.R B.{y|y≥}
C.{y|y≤} D.{y|0<y≤}
4.若二次函数y=ax2+bx+c的图象与x轴交于A(-2,0),B(4,0)两点,且函数的最大值为9,则这个二次函数的表达式是________________.
课堂巩固
1.一个面积为100 cm2的等腰梯形,上底长为x cm,下底长为上底长的3倍,则把它的高y表示成x的函数为( )
A.y=50x(x>0) B.y=100x(x>0)
C.y=(x>0) D.y=(x>0)
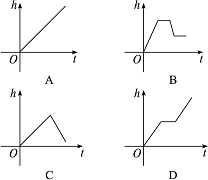
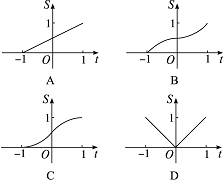
2.(2009全国重点中学领航卷,7)为悼念四川汶川地震中遇难同胞,在全国哀悼日第一天,某校升旗仪式中,先把国旗匀速升至旗杆顶部,停顿3秒钟后再把国旗匀速下落至旗杆中部.能正确反映这一过程中,国旗上升的高度h(米)与升旗时间t(秒)的函数关系的大致图象是〔设国旗的起始位置为h=0(米)〕…( )
3.(2009山东滨州高一期末测试,8)某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A.13立方米 B.14立方米
C.18立方米 D.26立方米
4.设f(x)=则f{f[f(-)]}的值为________,f(x)的定义域是________.
5.设函数f(x)满足f(x)+2f()=x(x≠0),求f(x).
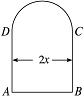
6.用长为l的铁丝弯成下部为矩形,上部为半圆形的框架(如右图).若矩形底边长为2x,求此框架围成的面积y与x的函数关系式,并指出其定义域.
![]()
1.设集合A={x|0≤x≤6},B={y|0≤y≤2},则从A到B的对应法则f不是映射的是( )
A.f:x→y=x B.f:x→y=x
C.f:x→y=x D.f:x→y=x
2.(2009浙江台州一模,文8)已知函数f(x)=若f(a)=f(4),则实数a等于……
( )
A.4 B.1或-1
C.-1或4 D.1,-1或4
3.(2008山东高考,文5)设函数f(x)=则f[]的值为… ( )
A. B.- C. D.18
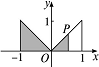
4.在函数y=|x|(x∈[-1,1])的图象上有一点P(t,|t|),此函数与x轴、直线x=-1及x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图可表示为( )
5.2008年北京成功举办了第29届奥运会,中国取得了51金、21银、28铜的骄人成绩.下表为北京奥运会官方票务网站公布的几种球类比赛的门票价格,某球迷赛前准备用12 000元预定15张下表中球类比赛的门票:
|
比赛项目 |
票价(元/场) |
|
男篮 |
1 000 |
|
足球 |
800 |
|
乒乓球 |
500 |
若在准备资金允许的范围内和总票数不变的前提下,这个球迷想预定上表中三种球类门票,其中足球门票数与乒乓球门票数相同,且足球门票的费用不超过男篮门票的费用,则可以预订男篮门票数为( )
A.2 B.3 C.4 D.5
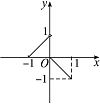
6.已知函数f(x)的图象如右图所示,则f(x)的解析式是________.
7.设函数f(x)=若
f(-4)=f(0),f(-2)=-2,则f(x)的解析式f(x)=__________.
8.已知集合A中的元素(x,y)在映射f的作用下与集合B中的元素(,)相对应,则与B中的元素(0,3)相对应的A中的元素是________.
9.一个弹簧不挂物体时长12 cm,挂上物体后会伸长,伸长的长度与所挂物体的质量成正比例.如果挂上3 kg物体后弹簧总长是13.5 cm,求弹簧总长y(cm)与所挂物体质量x(kg)之间的函数关系式.
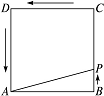
10.如图,动点P从边长为4的正方形ABCD的顶点B开始,顺次经C、D、A绕周界运动,用x表示点P的行程,y表示△APB的面积,求函数y=f(x)的解析式.
答案与解析
1.2.2 函数的表示法
课前预习
1.B y=-|x|=其图象是x轴下方的两条线段,包括x=±2时的两个端点.
2.B A到B的映射f:A→B,需满足集合A中任何一个元素在集合B中都有唯一确定的元素与之对应才行.
3.D 令u=x2+2,则u≥2.借助反比例函数y=的图象,易得0<y≤.
4.y=-(x+2)(x-4) 设y=a(x+2)(x-4),对称轴x=1,当x=1时,ymax=-9a=9,a=-1.
课堂巩固
1.C 由·y=100,得2xy=100.
∴y=(x>0).
2.B 国旗的运动规律是:匀速升至旗杆顶部——停顿3秒——国旗匀速下落至旗杆中部.对应的图象为B.
3.A 该单位职工每月应缴水费y与实际用水量x满足的关系式为y=
由y=16m,可知x>10.
令2mx-10m=16m,得x=13(立方米).
4. {x|x≥-1且x≠0} ∵-1<-<0,∴f(-)=2×(-)+2=.而0<<2,
∴f()=-×=-.
∵-1<-<0,∴f(-)=2×(-)+2=.因此f{f[f(-)]}=.函数f(x)的定义域为{x|-1≤x<0}∪{x|0<x<2}∪{x|x≥2}={x|x≥-1且x≠0}.
5.解:∵f(x)+2f()=x,①
以代换x得f()+2f(x)=.②
解①②组成的方程组得f(x)=-.
6.解:由题意知此框架围成的面积是由一个矩形和一个半圆组成的图形的面积,而矩形的长AB=2x,宽设为a,则有2x+2a+πx=l,即a=-x-x,半圆的直径为2x,半径为x.
所以y=+(-x-x)·2x=-(2+)x2+lx.
根据实际意义知-x-x>0,因x>0,解得0<x<,即函数y=-(2+)x2+lx的定义域是{x|0<x<}.
课后检测
1.A 对于答案A,当A中的元素x=6时,在B中没有元素与之对应.
2.C 由题意,得f(4)=4-3=1.当a>0时,由a-3=1,得a=4;当a≤0时,由a2=1,得a=-1.综上可知,a=-1或4.
3.A ∵f(2)=22+2-2=4,∴=.
∴f()=1-()2=,
即f[]=.
4.B 当t<0时,S=-,所以图象是开口向下的抛物线,顶点坐标是(0,);当t>0时,S=+,开口是向上的抛物线,顶点坐标是(0,).所以B满足要求.
5.D 设足球门票数与乒乓球门票数都预定n(n∈N*)张,则男篮门票数为(15-2n)张,
得
解得4≤n≤5.
由n∈N*,可得n=5,15-2n=5.
6.f(x)= 提示:∵f(x)的图象是由两条线段组成,
∴由一次函数解析式的求法可得.
7. 由题意,得⇒
∴f(x)=
8.(3,-3) 由题意得=0,=3,解得x=3,y=-3,即与元素(0,3)相对应的元素是(3,-3).
9.解:设所求函数解析式为y=kx+12,把x=3,y=13.5代入,得13.5=3k+12,k=.
所以所求的函数解析式为y=x+12.
点评:若已知条件告诉了我们曲线的种类和方程的具体形式,可先设出相应的函数解析式,然后根据题设条件列出方程或方程组,通过解方程或方程组求出待定系数,即得函数解析式,这种方法就是待定系数法.
10.解:当点P在BC上运动,即0≤x≤4时,y=×4x=2x;
当点P在CD上运动,即4<x≤8时,y=×4×4=8;
当点P在DA上运动,即8<x≤12时,y=×4×(12-x)=24-2x.
综上可知,f(x)=
点评:有些函数,在它的定义域中对于自变量x的不同取值区间,对应关系也不相同,这样的函数通常称为分段函数.分段函数是一个函数,而不是几个函数.处理分段函数问题时,要首先确定自变量的取值属于哪个区间,然后再按相应的对应关系进行解答.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

