北京师范大学亚太实验学校

2013～2014学年第二学期期中考试

2014.4

初一数学试卷

试卷说明:本次考试满分100分,考试时间 100分钟。

一、精心选一选（每小题3分，共30分）

1．在平面直角坐标系中，点P（2，3）在                               （　　 ）

A．第一象限    B．第二象限     C．第三象限       D．第四象限

2．下列各数中是无理数的是                                           （    ）

A． 3          B.           C.             D.

33．观察下图，在A、B、C、D四幅图中，能通过图(1)的平移得到的是     （      ）

  

 

 

 

4．4的平方根是                                                   （    ）

       A.±2           B. 2             C. －2            D. ±

5．已知点在轴上，则                               （     ）

A.0            B. 1            C. 2                D. 3

6. 如果不等式（－3）x＞－3的解集是x＞1，那么的取值范围是        （　  　）

A．＜3　              B．＞3　              C．＜0　              D．＞0

7．下列选项中，可以用来证明命题“”是假命题的反例是（     ）.

A.        B.          C.            D.

8．若a、b为实数，且满足|a－2|＋＝0，则b－a的值为             （      ）

（A）0       （B）2        （C）－2          （D）以上都不对

9．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）.

A. 30°                B. 25°            C. 20°          D. 15°      

 

10．把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是

                                                                     （    ）

 

 

 

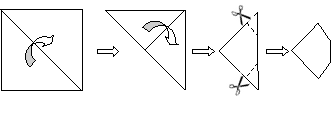A．六边形                   B．八边形                   C．十二边形               D．十六边

 

二．耐心填一填（每小题2分,共20分）

11.把命题“对顶角相等”改写成“如果……，那么……”的形式：___________________________________________________________________．

12.化简：=               ．

13．如图，已知 的度数是_______．

14．若实数a、b满足+5|b|=7,则S=-3|b|的取值范围是               　   ．

15.如图，将边长为2个单位长度的等边△ABC沿边BC向右平移1个单位长度得到△DEF，则四边形ABFD的周长为＿＿＿＿＿＿个单位长度．

 

 

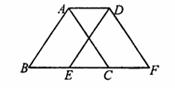
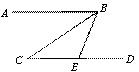
（第13题）                   （第15题）                     （第17题）

16.已知点，，点在轴上，且△ABC的面积为6，则点的坐标是　　　　　　.

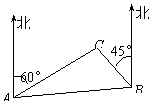
17. 如图，岛在岛的北偏东方向，在岛的北偏西方向，则＝________．.

18.若在实数范围内有意义，则的取值范围是__________．

19.如图所示，把直角梯形ABCD沿AD方向平移到梯形EFGH，HG=24 cm，

WG=8 cm，WC=6 cm，求阴影部分的面积为__________cm².

 

 

 

 

 

 

 

 

 

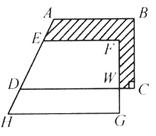
	19题图		20题图

 

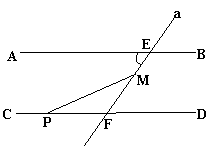
20. 已知，如图，AB∥CD，直线a交AB、CD分别于点E、F，点M在线段EF上，P是直线CD上的一个动点，（点P不与F重合）

（1）当点P在射线FC上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：____________________________．

（2）当点P在射线FD上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：

____________________________．

三、解答题（共50分）

21. （每小题4分）

（1）已知：，求的值．

 

 

 (2).计算   

 

 

22（本题4分）解不等式并将解集在数轴上表示出来．

 

 

 

 

 

 

 

 

 

23．（本小题 5分）

       完成下面的证明.

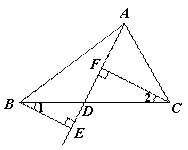已知：如图， D是BC上任意一点，BE⊥AD，交AD的

延长线于点E，CF⊥AD，垂足为F. 

求证：∠1＝∠2.

证明：∵BE⊥AD ，                                               

∴∠BED＝         °（                     ）.

∵CF⊥AD，

∴∠CFD＝         °.

∴∠BED＝∠CFD.

∴BE∥CF（                                    ）.

∴∠1＝∠2（                                   ）.

24．(本题4分)计算：

 

 

 

25．( 本题5分）解不等式组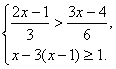并求出不等式组的整数解．

 

 

 

 

 

 

 

 

 

 

 

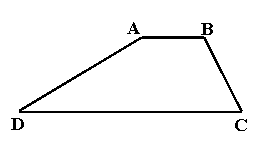26. （本题3分）

     （1）作BE∥AD交DC于E；

（2）连接AC，作BF∥AC

交DC的延长线于F；

（3）作AG⊥DC于G．

 

 

 

 

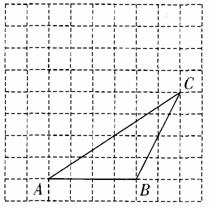
27．（本题4分）如图，在边长为1个单位的小正方形组成的网格中，△ABC的顶点都在小正方形的顶点上．

（1）       求出△ABC的面积；

（2）将△ABC向左平移2个单位，再向上平移4个单位．请在图中画出平移后的△A′B′C′及△A′B′C′的高C′D′.

 

 

 

 

2    28. （本题5分）某市统计资料表明，现在该市的城市建成区面积为1500平方千米，城市建成区园林绿地率为15%，计划五年后，该市城市建成区面积增加400平方千米，并且城市建成区园林绿地率超过20%，那么该市计划增加的城市建成区园林绿地面积应超过多少平方千米？

 

29.（本小题6分）

在平面直角坐标系xOy中，A（－3，0），B（1，4），BC∥y轴，与x轴相交于点C ，

BD∥x轴，与y轴相交于点D.

（1）如图1，直接写出 ① C点坐标               ，② D点坐标              ；

（2）如图1，直接写出△ABD的面积               ；

（3）在图1中，平移△ABD，使点D的对应点为原点O，点A、B的对应点分别为点A′、B′，画出图形，并解答下列问题：

①AB与A′B′的关系是：                                    ，

②四边形A A′OD的面积为               ；

（4）如图2，H（－2）是AD的中点，平移四边形ACBD使点D的对应点为DO的中点E，

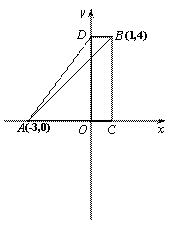
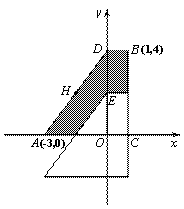直接写出图中阴影部分的面积是              .

 

 

 

 

 

 

 

 

 

 

	图1
			图2

30. （本小题 6 分）

如图，在四边形ABCD中，AB∥CD ，∠A＝110°，∠ABC＝∠ADC，BE平分∠ABC，与CD相交于点E ，DF平分∠ADC ，与AB相交于点F.

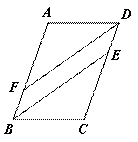（1）求证：BE∥DF；

（2）求∠BED的度数.

 

 

 

 

自学探究（每题4分）

1.若不等式组无解，则的取值范围是                         (       )

  A．     B.     C.     D.

2. 若关于x的不等式组的整数解共有4个，则m的取值范围是   (        )

A . 6 < m < 7      B. 6 ≤ m < 7   C. 6 ≤ m ≤ 7   D. 6 < m ≤ 7

 

 

3.由一些正整数组成的数表如下（表中下一行中数的个数

    是上一行中数的个数的2倍）：

第1行	2
第2行	4   6
第3行	8  10  12  14
…	…

若规定坐标号（）表示第行从左向右第个数，则（7，4）所表示的数是_______；

数2012对应的坐标号是______.    

 

4.已知两个整数a、b，满足0且a、b是整数，那么数对（a,b）有____________个.

 

 

 

 

 

5.现有100个整数，同时满足下列四个条件：

①；

②；

③；

④.

求的平方根.

 

 

 

 

6. 在平面直角坐标系中，我们把横 、纵坐标都是整数的点叫做整点．已知点，点是轴正半轴上的整点，记内部（不包括边界）的整点个数为．

当时，点的横坐标的所有可能值是          ；当点的横坐标为（为正整数）时，         （用含的代数式表示）.

附加题（4分）

已知四边形AOCD是放置在平面直角坐标系内的梯形，其中O是坐标原点，点A，C，D的坐标分别为（0,8），（5,0），（3,8）.若点P在梯形内，且△PAD的面积等于△POC的面积，

△PAO的面积等于△PCD的面积.请直接写出点P的坐标                   .

 

 

 

 

 

     友情提示：请你做完试卷后，再认真仔细地检查一遍，预祝你考出好成绩！

 

初一数学试题参考答案及评分标准

一、选择题（共10个小题，每小题3分，共30分）

题号	1	2	3	4	5	6	7	8	9	10
答案	A	D	C	A	B	D	A	C	B	C

二、填空题（共10个小题，每小题2分，共20分).

11．如果两个角是对顶角,那么这两个角相等.     12．         13．        

 14．. 0,1,2      15.  8         16. (0,4) 或（0，-4 ）      17．        18．.x2          19．168         20．（1）当点P在射线FC上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：

_∠FMP+∠FPM =∠AEF _______；

（2）当点P在射线FD上移动时，∠FMP、∠FPM和∠AEF之间的数量关系是：

_∠FMP+∠FPM +∠AEF=180° _____；

三、解答题（共50分）

21．(1)

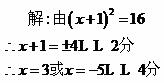               …………………………4分              

(2)

22

．

23

90，垂直定义    ………………………………………………………………………2分

90    ………………………………………………………………………3分

内错角相等，两直线平行  ………………………………………………4分

     两直线平行，内错角相等  ………………………………………5分

24

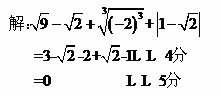
25

26

27．（1）△ABC的面积是8┉┉2分

    （2）图略，┉┉5分

28. 解：设该市计划增加的城市建成区园林绿地面积应为x平方千米.   ………………………………1分

根据题意，得

          ……………………………………………………3分

 

解得  x＞155.   ……………………………………………………5分

 

答：该市计划增加的城市建成区园林绿地面积应超过155平方千米.

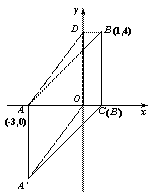
29.（1）①（1,0）， ……………………………………………………1分

②（0,4）； ……………………………………………………2分

（2）2； ……………………………………………………………3分

（3）如图；…………………………………………………………4分

① AB∥A′B′，AB＝A′B′；  …………………………………5分

② 12；  ………………………………………………………6分

（4）.  …………………………………………………………7分

 

 

30. （1）证明：<, /span>∵BE平分∠ABC，DF平分∠ADC，

∴∠FBE＝∠ABC，∠FDE＝∠ADC. ……………1分

∵∠ABC＝∠ADC ，

∴∠FBE＝∠FDE.     …………………………………2分

∵AB∥CD ，

∴∠FBE+∠BED=180°. …………………………………3分

∴∠FDE+∠BED=180°.

∴BE∥DF.  ………………………………………………4分

（2）解：∵AB∥CD ，

∴∠A+∠ADC＝180°.   ………………………5分

∵∠A＝110°，

∴∠ADC＝70°.

∴∠FDE＝∠ADC＝35°.

∵BE∥DF，

∴∠BED=180°－∠FDE＝145°.  ………………………6分

 

 

自学能力测试：

1,B.2,D.3, 134；（10，495）4. 7  5. (20个2,50个1，30个-1) 6 3或4 m=6n-3

解：如图：

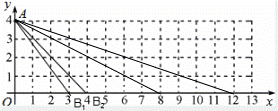
当点B在（3，0）点或（4，0）点时，△AOB内部（不包括边界）的整点为（1，1）（1，2）（2，1），共三个点，
所以当m=3时，点B的横坐标的所有可能值是3或4；
当点B的横坐标为8时，n=2时，△AOB内部（不包括边界）的整点个数m=

(4×2+1−2)×3−3

2

=9，
当点B的横坐标为12时，n=3时，△AOB内部（不包括边界）的整点个数m=

(4×3+1−2)×3−3

2

=15，
所以当点B的横坐标为4n（n为正整数）时，m=

(4×n+1−2)×3−3

2

=6n-3；
另解：网格点横向一共3行，竖向一共是4n-1列，所以在y轴和4n点形成的矩形内部一共有3（4n-1）个网格点，而这条连线为矩形的对角线，与3条横线有3个网格点相交，所以要减掉3点，总的来说就是矩形内部网格点减掉3点的一半，即为[3（4n-1）-3]÷2=6n-3．
故答案为：3或4，6n-3．

附加题

如图，过点P作PE⊥y轴于点E。

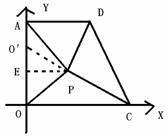因为⊿PAD的面积等于⊿POC的面积，

所以3AE=5OE，即3（8-OE）=5OE，解得OE=3

所以⊿PAD的面积=⊿POC的面积= ×3×5=7.5

⊿PAO的面积=⊿PCD的面积= [﹙3﹢5﹚×8÷2－2×7.5 ] ÷2=8.5

则×8PE=8.5，即PE=

所以点P的坐标是（，3）