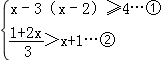2014年春季学期旧莫初级中学八年级数学期中测试

数学

（总分：100分   考试时间：120分钟）

班级          姓名            得分            

一、选择题（每小题3分，共24分）

1、△ABC的三个内角度数之比是1：2：3，则它是（  ）

  A、锐角三角形  　B、直角三角形  　C、钝角三角形  　　D、等边三角形

2、等腰三角形的一边长等于4，一边长等于9，则它的周长是（  ）

  A、17         　 B、22         　 C、17或22    　　D、13

3、若>,则下列不等式中正确的是（    ）                                             

A、     B、   C、    D、

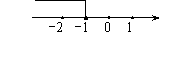4、关于x的不等式2x－a≤－1

的解集如图所示，则a的取值是（     ）

A、0          B、－3       　　　 C、－2       　  D、－1

5、把不等式组的解集表示在数轴上，正确的是（    ）                       

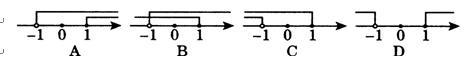
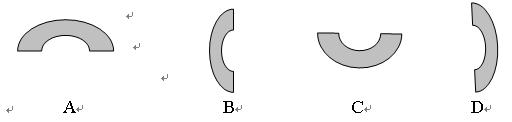
6、下列图形中，是由(1)仅通过平移得到的是(　　)

　

7、将图形 按顺时针方向旋转90^o后的图形是(  )           

 

 

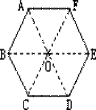
8、如图可以看作正△OAB绕点O通过(　　)旋转所得到的

A、3次　      　      B、4次　　

 C、5次　     　       D、6次

二、填空题（每小题3分，共21分）

9、x的与12的差不小于6，用不等式表示为__________________；

10、若关于的方程组的解满足>，则P的取值范围是_________；

11、不等式组的整数解是______________；

12、如图，图案绕中心旋转_______度(填最小度

数) 和原来图案互相重合.

13、如图，把大小相等的两个长方形拼成L形图案，则∠FCA＝          度。

 

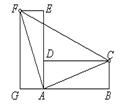
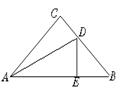
			第15题
	第14题

 

14、如图，在△ABC中，∠C=90°，AD是角平分线，DE⊥AB于E，且DE=2 cm，

BD=4 cm，则BC=_____cm.

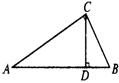
15、如图，∠ACB＝90°，CD⊥AB，∠A＝30°，BD＝2cm，则AB=          cm；

三、解答题（共55分）

16、解下列方程（组）并把解集表示在数轴上：

（1）（4分）3x﹣4﹥2x﹣1；      （2）（4分）﹣3x﹢4≤x﹣8；

 

 

 

（3）（5分）       （4）（5分）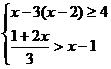

 

 

 

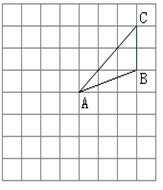
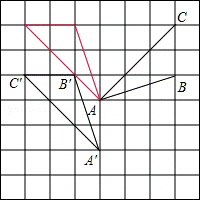
17、（5分）如图所示，在边长为1的网格中

作出 △ABC 绕点A按逆时针方向旋转90o

再向下平移2格后的图形△A₁B₁C₁

 

 

 

18、（7分）已知关于的方程的解是非正数，求的取值范围

 

 

 

 

 

 

 

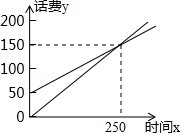
19、（9分）我市移动通讯公司开设了两种通讯业务，A类是固定用户：先缴50元基础费，然后每通话1分钟再付话费0.4元；B类是“神州行”用户：使用者不缴月租费，每通话1分钟会话费0.6元（这里均指市内通话）；如果一个月内通话时间为分钟，分别设A类和B类两种通讯方式的费用为，

（1）写出、与之间的函数关系式；

（2）一个月内通话多少分钟，用户选择A类合算？还是B类合算？

（3）若某人预计使用话费150元，他应选择哪种方式合算？

 

 

 

 

 

 

 

 

 

 

 

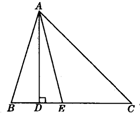20、（8分）如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，∠C=45°，求∠DAE与∠AEC的度数．

 

 

 

 

21、（8分）如图，已知，在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于

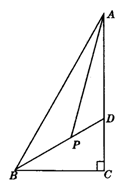D。（1）若∠BAC=30°，求证：AD=BD；（2）若AP平分∠BAC且交BD于P，求

∠BPA的度数．

 

 

 

 

 

 

 

 

 

 

 

 

 , ;

 

参考答案

一、选择题（每小题3分，共24分）

1．B

2．B

3．B

4．D

5．B

6．C

7．D

8．C

二、填空题（每小题3分，共21分）

9．　x﹣12≥6　．

10．
　p＞﹣6　．

11．　0，1　．

12．　60　度．

13．　45　度．

14．　6　cm．

15．　8　cm．

三、解答题（共55分）

16．	解：（1）移项，得：3x﹣2x＞4﹣1， 合并同类项，得：x＞3；   （2）移项，得：﹣3x﹣x≤﹣8﹣4， 合并同类项，得：﹣4x≤﹣12， 系数化成1得：x≥3； （3）， 解①得：x≤4， 解②得：x≤， 则不等式组的解集是：x≤；   （4）， 解①得：x≤1， 解②得：x＜﹣2， 则不等式组的解集是：x＜﹣2．
17．	解：如图所示，红色三角形为△ABC绕点A按逆时针方向旋转90°的三角形， △A′B′C′即为所要求作的三角形．
18．	解：方程， 2x+2m﹣6x+3=6m， ﹣4x=4m﹣3， x=﹣． 因为它的解为非正数，即x≤0， ∴﹣≤0， 得m≥．
19．	解：（1）y1、y2与x之间的函数关系式分别为：y1=0.4x+50，y2=0.6x   （2）x≥250分钟，用户选择A类不吃亏 当一个月内通话x≤250分钟，用户选择B类不吃亏   （3）如图可知若某人预计使用话费150元， 故他应选择A、B两种方式都同样合算．
20．	解：方法1： ∵∠B+∠C+∠BAC=180°，∠B=75°，∠C=45°， ∴∠BAC=60°， ∵AE平分∠BAC， ∴∠BAE=∠CAE=∠BAC=×60°=30°， ∵AD是BC上的高， ∴∠B+∠BAD=90°， ∴∠BAD=90°﹣∠B=90°﹣75°=15°， ∴∠DAE=∠BAE﹣∠BAD=30°﹣15°=15°， 在△AEC中，∠AEC=180°﹣∠C﹣∠CAE=180°﹣45°﹣30°=105°；   方法2：同方法1，得出∠BAC=60°． ∵AE平分∠BAC， ∴∠EAC=∠BAC=×60°=30°． ∵AD是BC上的高， ∴∠C+∠CAD=90°， ∴∠CAD=90°﹣45°=45°， ∴∠DAE=∠CAD﹣∠CAE=45°﹣30°=15°． ∵∠AEC+∠C+∠EAC=180°， ∴∠AEC+30°+45°=180°， ∴∠AEC=105°． 答：∠DAE=15°，∠AEC=105°．
21．	（1）证明：∵∠BAC=30°，∠C=90°， ∴∠ABC=60°． 又∵BD平分∠ABC， ∴∠ABD=30°， ∴∠BAC=∠ABD， ∴BD=AD．   （2）解法一：∵∠C=90°， ∴∠BAC+∠ABC=90°， ∴（∠BAC+∠ABC）=45°． ∵BD平分∠ABC，AP平分∠BAC， ∠BAP=∠BAC，∠ABP=∠ABC，即∠BAP+∠ABP=45° ∴∠APB=180°﹣45°=135°．   解法二：∵∠C=90°， ∴∠BAC+∠ABC=90°， ∴（∠BAC+∠ABC）=45°． ∵BD平分∠ABC，AP平分∠BAC， ∠DBC=∠ABC，∠PAC=∠BAC， ∴∠DBC+∠PAD=45°． ∴∠BPA=∠PDA+∠PAD =∠DBC+∠C+∠PAD =∠DBC+∠PAD+∠C =45°+90° =135°．