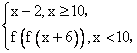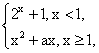| 上传:席俊雄数学 | 审核发布:admin | 更新时间:2015-10-20 15:26:01 | 点击次数:602次 |
上课时间:2015年 月 日 学期总第 课时
|
课 题 |
函数及其表示 |
课 型 |
讲评课 |
|
|
课 时 |
第 2 课时 |
主备课人 |
周 思 |
|
|
复备课人 |
陈雄武 |
审核人 |
雷淇未 |
|
|
课前准备 |
|
|||
|
教 学 目 标 |
1.了解构成函数的要素,了解映射的概念,会求一些简单函数的定义域和值域. 2.理解函数的三种表示法:解析法、图象法和列表法,能根据不同的要求选择恰当的方法表示简单的函数. 3.了解分段函数,能用分段函数来解决一些简单的数学问题. |
|||
|
教学重点 |
函数的概念 |
|||
|
教学难点 |
|
|||
|
教学过程和教学内容 |
二次备课 |
|||
|
一、典例分析 1.下列四组中的函数f(x)与g(x)表示相等函数的是( ) (A)f(x)=x,g(x)=( (C)f(x)=x,g(x)= 3.函数f(x)= (A)(- 4.设f(x)= (A)10 (B)11 (C)12 (D)13 5.定义运算a (A)(0,2] (B)(0,3] (C)(0,1] (D)[1,2] 6.如果 (A) 7.已知g(x)=1-2x,f(g(x))= (A)15 (B)1 (C)3 (D)30 8.函数f(x)= (A)3 (B)-3 (C)3或-3 (D)5或-3 9.已知函数y=f(x+1)的定义域是[-2,3],则y=f(2x-1)的定义域是( ) (A)[0, 10.(能力挑战题)已知函数y=f(x)的图象关于直线x=-1对称,且当x∈(0,+∞)时,有f(x)= (A)f(x)=- 11.已知函数f(x)= 12.已知f(x)= 13.如果对任意实数x,y,都有f(x+y)=f(x)·f(y),且f(1)=2, (1)求f(2),f(3),f(4)的值. (2)求
二、课时作业:预习金版13-15
|
|
|||
|
教学札记: |
||||
东安一中教务处设计
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1