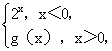课  题

指数函数

课  型

讲评课

课  时

第  2  课时

主备课人

周 思

复备课人

陈雄武

审核人

雷淇未

课前准备

教 学 目 标

1．了解指数函数模型的实际背景.

2．理解有理指数幂的含义，了解实数指数幂的意义，掌握幂的运算.

3．理解指数函数的概念，会求与指数函数性质有关的问题.

教学重点

掌握幂的运算,理解指数函数的概念，会求与指数函数性质有关的问题.

教学难点

求与指数函数性质有关的问题

教学过程和教学内容

二次备课

一、典例分析

1.函数y=(a>1)的图象的大致形状是(　　)

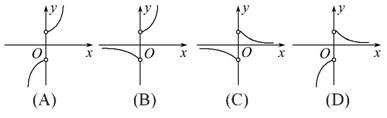
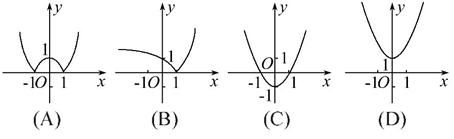
2.(2013·韶关模拟)设a=2^2.5,b=2.5⁰,c=()^2.5,则a,b,c的大小关系是(　　)

(A)a>c>b　　　　　(B)c>a>b

(C)a>b>c                (D)b>a>c

3.设函数f(x)=若f(x)是奇函数,则g(2)的值是(　　)

(A)-　　  (B)-4　 　(C)　   　(D)4

4.(2013·郑州模拟)已知函数f(x)=2^x-2,则函数y=|f(x)|的图象可能是(　　)

5.(2013·永州模拟)函数y=的值域是(   )

(A)［0,+∞)       (B)［1,+∞)

(C)(-∞,+∞)      (D)［，+∞)

6.已知f(x)=2^x+2^-x,若f(a)=3,则f(2a)=(　　)

(A)5　　(B)7　　(C)9　　(D)11

7.若函数f(x)=(a+)cosx是奇函数,则常数a的值等于(　　)

(A)-1       (B)1        (C)-      (D)

8.函数y=|2^x-1|在区间(k-1,k+1)内不单调,则k的取值范围是(　　)

(A)(-1,+∞)         (B)(-∞,1)

(C)(-1,1)           (D)(0,2)

9.若函数f(x)=a^|2x-4|(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是(　　)

(A)(-∞,2]          (B)[2,+∞)

(C)[-2,+∞)         (D)(-∞,-2]

10.(能力挑战题)设函数f(x)定义在实数集上,它的图象关于直线x=1对称,且当x≥1时,f(x)=3^x-1,则有(　　)

(A)f()))

(B)f()))

(C)f()))

(D)f()))

11.(2013·衡阳模拟)已知a=,函数f(x)=a^x,若实数m,n满足f(m)＞f(n),则m,n的大小关系为　　　.

12.设偶函数f(x)满足f(x)=2^x-4(x≥0),则不等式f(x)>0的解集为　　　　.

13.(2013·杭州模拟)已知0≤x≤2,则y=-3·2^x+5的最大值为　　　　.

14.(能力挑战题)设定义在R上的函数f(x)同时满足以下条件:①f(x)+f(-x)=0;②f(x)=f(x+2);③当0≤x≤1时,f(x)=2^x-1,则f()+f(1)+f()+f(2) +f()=　　　　.

15.(能力挑战题)已知定义域为R的函数f(x)=是奇函数.

(1)求a,b的值.

(2)用定义证明f(x)在(-∞,+∞)上为减函数.

(3)若对于任意t∈R,不等式f(t²-2t)+f(2t²-k)<0恒成立,求k的范围.

二、课时作业 预习金版 18-20

教学札记：