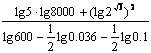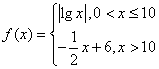课  题

对数函数

课  型

复习课

课  时

第   1   课时

主备课人

周  思

复备课人

陈雄武

审核人

雷淇未

课前准备

教 学 目 标

1．理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；了解对数在简化运算中的作用.

2．理解对数函数的概念；会求与对数函数性质有关的问题.

教学重点

掌握对数的运算,理解对数函数的概念，会求与对数函数性质有关的问题.

教学难点

求与对数函数性质有关的问题

教学过程和教学内容

二次备课

一、基础回扣

（1）指数式与对数式的关系：

a^b=N            ， 其中，

（2）对数运算性质: （M＞0，N＞0，a＞0，a≠1）

①log_a（MN）=            ②log_a=          

③log_aMⁿ=            

（3）对数换底公式：（a＞0，a≠1，b＞0，b≠1，N＞0）

log_bN=             .

 (4) 对数恒等式：（a＞0，a≠1，N＞0）

（5）对数函数y=log_ax的图象和性质

二、典例突破

考向 1  对数的运算 

【典例1】计算:（1）；       2

  （2）；            4/5

（3）                   3/4

 考向 2  对数函数的图象及其应用 

【典例2】(1)(2013·长沙模拟)函数y=ax²+bx与  (ab≠0,|a|≠b)在同一直角坐标系中的图象可能是(　　)

(2)已知函数

f(x)= ,若a,b,c互不相等，且f(a)=f(b)=f(c)，则abc的取值范围是(   )

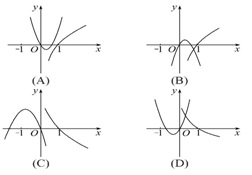
(A)(1,10)         (B)(5,6)      (C)(10,12)        (D)(20,24)

考向 3 对数函数的性质及应用 

【典例3】已知函数f(x)=              .

(1)求函数f(x)的定义域.

(2)若函数f(x)的定义域关于坐标原点对称,试讨论它的奇偶性和单调性.

【创新体验】数形结合解决恒成立问题 

【典例】(2012·新课标全国卷)当0＜x≤ 1/2 时，4^x＜log_ax，

则a的取值范围是(   )

(A)(0，)        (B)(，1)     (C)(1,)        (D)(，2

三、知能巩固

1.(2012·天津)已知a=2¹²，b=(1/2)^-0.5，c=2log₅2,则a，b，c的大小关系为

(A)c＜b＜a           (B)c＜a＜b

(C)b＜a＜c           (D)b＜c＜a

2.（2013·衡阳模拟）设函数f（x）=log_ax（a＞0,a≠1）,若f（x₁·x₂·…·x_n）=8，则f（x₁²）+f（x₂²）+…+f（x_n²）=      （   ）

（A）4   （B）8   （C）16   （D）2log_a8

四．课时作业

教学札记：