学习目标

说明建构种群增长模型的方法

学习重点

尝试建构种群增长的数学模型，并据此解释种群数量的变化

学习难点

说明建构种群增长模型的方法

学生活动

教学设计

自

主

研

讨

目标与导入

1．建构种群增长模型的方法

（1）数学模型定义：____________________________

（2）建立数学模型包括以下步骤： 2．种群增长的“J”型曲线

模型假设：__________________________________

建立模型：____________________________________

模型中各参数的意义：______________________________

自学与诊断

3．种群增长的“S”型曲线

概念：___________________________________________

K值：_____________________________________________

4．种群数量的波动和下降

大多数种群的数量总是在__________，在不利的条件下，种群数量还会______

合 

作

互

动

互动与展示

1．问题探讨

（1）计算n代细菌数量的计算公式Nn＝_______，x小时后，由一个细菌分裂产生的细菌数量应

是＝_________

（2）细菌种群数量按此速度繁殖的条件是_________________________________，试分析如果在一个培养基中，细菌的数量将如何变化？______________________________。

2．建构种群增长的数学模型的方法

以“问题探讨”中实验条件下细菌种群数量的变化为例，得到的可用来描述该种群数量变化的数学模型是：

（1）公式________________。

（2）种群数量增长曲线画在课本66页上。

精讲与点拨

3． 种群增长的“J”型曲线

（1）根据实例理解“J”型增长的数量变化特点：____________________________

（2）建构种群数量“J”型增长的数学模型

①模型假设：______________________。

②建立模型：如果种群的起始数量为N0，并且第二年的数量是第一年的λ倍，那么：一年后种群数量N1＝________，两年后种群数量N2＝________，t年后群数量Nt＝_____________。（这个公式即为数学模型），（3）思考：当λ>1、λ=1、1<λ<0、λ=0时，种群的数量变化分别会怎样？（4）自然界中“J”型增长能一直持续下去吗？原因是什么？

检

测

与

评

价

总结与升华

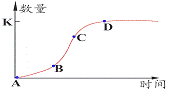
4．种群增长的“S”型曲线

（1）结合课本生态学家高斯的实验结果理解“S”型增长的特点：

（2）建构种群数量“S”型增长的数学模型

①模型假设：_____________________________________________

②建立模型。（种群增长的曲线图）①分别分析B点和D点时的出生率和死亡率情况。B点：出生率_____死亡率 D点：出生率_____死亡率

②一开始AB段数量增长慢的原因是____________________________

③数量增长最快的是__________段，其原因是_________________

④CD段增长速度变慢的可能原因是________________________

⑤D点达到最大值K值，K值的含义是__________________

⑥你认为K值是个固定值吗，为什么？

（4）试从环境容纳量上分析保护大熊猫和控制鼠害的根本措施

达标检测题

5．种群增长的“J”型曲线和“S”型曲线的比较

种群数量的波动和下降

（1）影响种群数量变化的因素有：_______________________等。

（2）大多数种群的数量总是在______________的，这些变化主要取决于_________变化

课后反思：