16.3 二次根式的加减

课型:               上课时间：                课时：          

学习内容：

    含有二次根式的单项式与单项式相乘、相除；多项式与单项式相乘、相除；多项式与多项式相乘、相除；乘法公式的应用．

学习目标：

 1、含有二次根式的式子进行乘除运算和含有二次根式的多项式乘法公式的应用．

 2、复习整式运算知识并将该知识运用于含有二次根式的式子的乘除、乘方等运算．

 学习过程

一、 自主学习 

（一）复习引入 

   1．计算   （1）（2x+y）·zx==           （2）（2x2y+3xy2）÷xy===         

2．计算  （1）（2x+3y）（2x-3y）        （2）（2x+1）2+（2x-1）2

===                         ===

（二）、探索新知

   如果把上面的x、y、z改写成二次根式呢？以上的运算规律是否仍成立呢？仍成立．

   例1．计算: （1）（+）×           （2）（4-3）÷2

             ===                                ===

例2．计算  （1）（+6）（3-）         （2）（+）（-）

        ===                                  ===

 二、巩固练习

    课本P20练习1、2．

三、学生小组交流解疑，教师点拨、拓展

1、例3．已知，X==2   化简+，并求值．

   解：原式==+

==+ 

==（x+1）+x-2+x+2

          ==4x+2

   当X==2时      ∴原式=4X2+2=10

   2、、归纳小结

    本节课应掌握二次根式的乘、除、乘方等运算．

四、课堂检测

 （一）、选择题      1．（-3+2）×的值是（  ）．

    A．-3   B．3-   C．2-     D．-

 2．计算（+）（-）的值是（  ）．A．2  B．3   C．4   D．1

 （二）、填空题    1．（-+）2的计算结果（用最简根式表示）是________．

2．（1-2）（1+2）-（2-1）2的计算结果（用最简二次根式表示）是_______．  

    3．若x=-1，则x2+2x+1=________．

    4．已知a=3+2，b=3-2，则a2b-ab2=_________．

    三、综合提高题

  1．化简

2．当x=时，求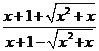+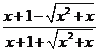的值．（用最简二次根式表示）

 课外知识 

   （1）、练习：下列各组二次根式中，是同类二次根式的是（  ）．

A．与   B．与    C．与  D．与

（2）、互为有理化因式：互为有理化因式是指两个二次根式的乘积是有理数，不含有二次根式：如2与就是互为有理化因式；+1与-1也是互为有理化因式．

  练习：1、+的有理化因式是________；

2、x-的有理化因式是_________．    3、  2的有理化因式是_______．