课题

10勾股定理2

教学目标

1、知识与方法目标：通过对一些典型题目的思考、练习，能正确、熟练的进行勾股定理有关计算，深入对勾股定理的理解。

2、过程与方法目标：通过对一些题目的探讨，以达到掌握知识的目的。

3、情感与态度目标：感受数学在生活中的应用，感受数学定理的美。

重点

勾股定理的实际应用

难点

熟练的应用勾股定理解决实际问题

教学环节

导学过程

学习过程

备注

自

主

探

究 

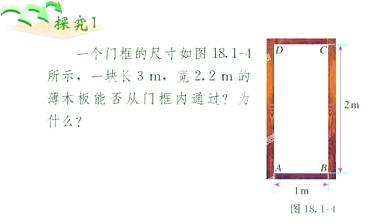
课前复习

1、勾股定理的内容是什么？

问：是这样的。在RtΔABC中，∠C＝90°，有：AC2+BC2＝AB2，勾股定理揭示了直角三角形三边之间的关系。

今天我们来看看这个定理的应用。

新课过程 

分析：

大家分组合作探究：

解：在RtΔABC中，由题意有：

　　AC＝ ＝ ≈2.236

　　∵AC大于木板的宽

　　∴薄木板能从门框通过。

学生进行练习： 

1、在Rt△ABC中，AB＝c，BC＝a，AC＝b， ∠B=90゜.

①已知a=5，b=12，求c；

②已知a=20，c=29，求b

（请大家画出图来，注意不要简单机械的套a2+b2＝c2，要根据本质来看问题）

2、如果一个直角三角形的两条边长分别是6厘米和8厘米，那么这个三角形的周长是多少厘米？

解：①当6cm和8cm分别为两直角边时；

　　斜边＝ ＝10

　　∴周长为：6+8+10＝24cm

②当6cm为一直角边，8cm是斜边时，

　　另一直角边＝  ＝2 

　　周长为：6+8+2 ＝14+2 

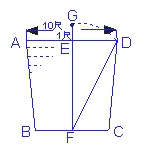
解：由题意有：∠O＝90°，在RtΔABO中

　　∴AO＝ ＝2.4（米）

　　又∵下滑了0.4米

　　∴OC＝2.0米

在RtΔODC中

∴OD＝ =1.5（米）

∴外移BD＝0.8米

答：梯足将外移0.8米。

例3 再来看一道古代名题：

这是一道成书于公元前一世纪，距今约两千多年前的，《九章算术》中记录的一道古代趣题：

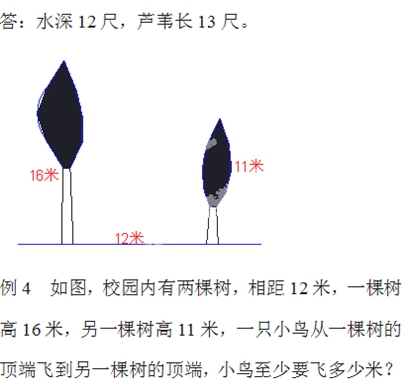
“现在有一个贮满水的正方形池子，池子的中央长着一株芦苇，水池的边长为10尺，芦苇露出水面1尺。若将芦苇拉到岸边，刚好能达到水池岸与水面的交接线的中点上。请求出水深与芦苇的长各有多少尺？

解：由题意有：DE＝5尺，DF＝FE+1。

设EF＝x尺，则DF＝（x+1）尺

由勾股定理有：

x2+52＝（x+1）2

解之得：x＝12

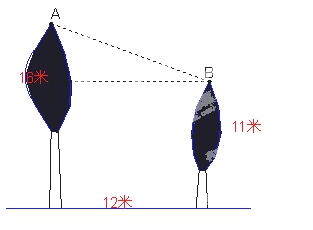
解：由题意有：BC＝12米，AC＝16－11＝5米。

在RtΔABC中

AB＝ ＝13

答：小鸟至少要飞13米。

三、作业：完成书P28页第3—6题

学生自主完成。做的同时回顾所学知识。

点评：找出不变量，分析问题的数量关系，通过已知和未知的联系，建构方程，最后解出方程

学生能够根据实际问题抽象出数学模型，能够根据已有知识解决问题

尝

试

应

用 

补

偿

提

高

达标检测  

巩固提升

作业布置

与

预习提纲

教

这节课，学生在惊险、有趣的氛围中主动经历了知识的发生、发展与联系

的全过程，从中领悟数学思想，获得成功的体验，逐步内化为自身的数学知识与技能，并会逐步提升为分析问题、解决问题的数学能力