| 上传:admin | 审核发布:admin | 更新时间:2015-3-22 17:20:41 | 点击次数:758次 |
勾股定理逆定理(二)
学习目标: 1.灵活应用勾股定理及逆定理解决实际问题。
2.进一步加深勾股定理与逆定理之间关系的认识
3.培养数学思维以及合情推理意识,感悟勾股定理和逆定理的应用价值
重点:灵活应用勾股定理及逆定理解决实际问题
难点:灵活应用勾股定理及逆定理解决实际问题

![]()
1.直角三角形有如下性质:(1)有一个角是____________;(2)两个锐角___![]() _________,
_________,
(3)两直角边_________________________:
![]() (4)在含30°角的直角三角形中,_
(4)在含30°角的直角三角形中,_![]() _____________________
_____________________
2. 如果一个三角形的三边长a,b,c,满足____________________,那么这个三角形是______________________
![]()
1.如果一个三角形的三边长a,b,c,满足________________________,那么这个三角形是______________________
2.应用勾股定理及逆定理解决问题时,应注意那些问题?
![]()
1.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m![]() 的方向是 。
的方向是 。
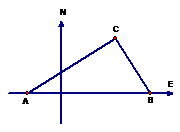 2.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A、B、C三点能否构成直角三角形?为什么?
2.如图,在操场上竖直立着一根长为2米的测影竿,早晨测得它的影长为4米,中午测得它的影长为1米,则A、B、C三点能否构成直角三角形?为什么?
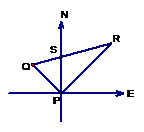
3.如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西40°,问:甲巡逻艇的航向?
![]()

1. ![]()
(探究点一
例1(P83例2)
分析:⑴了解方![]() 位角,及方位名词;
位角,及方位名词;
⑵依题意画出图形;
⑶依题意可得PR=12×1.5=18,PQ=16×1.5=24, QR=30;
⑷因为242+182=302,PQ2+PR2=QR2,根据勾股定理 的逆定理,知∠QPR=90°;
![]() ⑸∠PRS=∠QPR-∠QPS=45°。
⑸∠PRS=∠QPR-∠QPS=45°。
小结:养成“已知三边求角,利用勾股定理的逆定理”的意识。
探究点二
例2一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边
长7米,比较长边短1米,请你试判断这个三角形的形状。
分析: ⑴若判断三角形的形状,先求三角形的三边长;
⑵设未知数列方程,求出三角形的三边长;
⑶根据勾股定理的逆定理判断三角形的形状
小结:应用方程思想解决几何问题
(二)知识综合应用探究
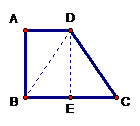 例3已知:如图,四边形ABCD,AD∥BC,AB=4,BC
例3已知:如图,四边形ABCD,AD∥BC,AB=4,BC![]() =6,CD=5,AD=3。
=6,CD=5,AD=3。
求:![]() 四边形ABCD的面积。
四边形ABCD的面积。
分析:⑴作DE∥AB,连结BD,则可以证明△ABD≌△EDB(ASA);
⑵DE=AB=4,BE=AD=3,EC=EB=3;
⑶在△DEC中,3、4、5勾股数,△DEC为直角三角形,DE⊥BC;
⑷利用梯形面积公式可解,或利用三角形的面积。
![]()
![]()
![]()
![]()
![]()
![]()

.
1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.等腰三角形;
B.直角三角形;
C.等腰三角形或直角三角形;
D.等腰直角三角形。
2.![]() 若△ABC的三边a、b、c,满足a:b:c=1:1:
若△ABC的三边a、b、c,满足a:b:c=1:1:![]() ,试判断△ABC的形状。
,试判断△ABC的形状。
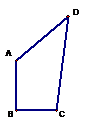 3.已知:如图,四边形ABCD,AB=1,BC=
3.已知:如图,四边形ABCD,AB=1,BC=![]() ,CD=
,CD=![]() ,AD=3,且AB⊥BC。
,AD=3,且AB⊥BC。
求:四边形ABCD的面积。
。
4.在△ABC中,AB=13cm,AC=24cm,中线B![]() D=5cm。求证:△ABC是等腰三角形。
D=5cm。求证:△ABC是等腰三角形。
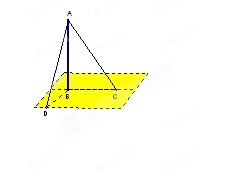
5![]() .一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电
.一根12米的电线杆AB,用铁丝AC、AD固定,现已知用去铁丝AC=15米,AD=13米,又测得地面上B、C两点之间距离是9米,B、D两点之间距离是5米,则电![]() 线杆和地面是否垂直,为什么?
线杆和地面是否垂直,为什么?
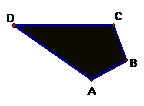
6.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测![]() 得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

