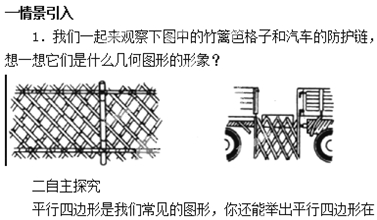
| 上传:admin | 审核发布:admin | 更新时间:2015-3-22 17:31:36 | 点击次数:646次 |
蒙 阴 四 中 教 师 教 案
|
课题 |
平行四边形的性质(1) |
||
|
教学目标 |
1. 理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质. 2. 会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证. 3. 培养学生发现问题、解决问题的能力及逻辑推理能力.
|
||
|
重点 |
平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
|
||
|
难点 |
运用平行四边形的性质进行有关的论证和计算.
|
||
|
教学环节 |
导学过程 |
学习过程 |
备注 |
|
自 主 探 究 |
你能总结出平行四边形的定义吗?
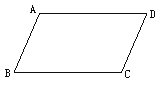
(2)表示:平行四边形用符号“ 如图,在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD记作“ ①∵AB//DC ,AD//BC , ∴四边形ABCD是平行四边形(判定);
②∵四边形ABCD是平行四边形∴AB//DC, AD//BC(性质).
注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.(教学时要结合图形,让学生认识清楚) 2.【探究】平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?我们一起来探究一下.
(2)猜想 平行四边形的对边相等、对角相等. 下面证明这个结论的正确性.
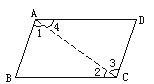
已知:如图 求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD. 分析:作 (作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.) 证明:连接AC, ∵ AB∥CD,AD∥BC, ∴ ∠1=∠3,∠2=∠4. 又 AC=CA, ∴ △ABC≌△CDA (ASA). ∴ AB=CD,CB=AD,∠B=∠D. 又 ∠1+∠4=∠2+∠3, ∴ ∠BAD=∠BCD. 由此得到: 平行四边形性质1 平行四边形的对边相等. 平行四边形性质2 平行四边形的对角相等.
三尝试应用
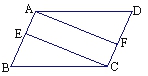
例2(补充)如图,在平行四边形ABCD中,AE=CF, 求证:AF=CE. 分析:要证AF=CE,需证△ADF≌△CBE,由于四边形ABCD是平行四边形,因此有∠D=∠B ,AD=BC,AB=CD,又AE=CF,根据等式性质,可得BE=DF.由“边角边”可得出所需要的结论. 证明略. 1.填空: (1)在 (2)如果
2.如图4.3-9,在
四课堂小结 本节课学习了哪些内容?
五补偿提高 1.(选择)在下列图形的性质中,平行四边形不一定具有的是( ). (A)对角相等 (B)对角互补 (C)邻角互补 (D)内角和是 2.在 (A)4个 (B)5个 (C)8个 (D)9个
|
学生回答
学生自己总结教师指导规范表示方法
让学生根据平行四边形的定义画一个一个平行四边形,观察这个四边形,它除具有四边形的性质和两组对边分别平行外以,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致? (1)由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为补角.
学生小组内讨论完成并总结平行四边形的性质
学生板演
学生分组完成
|
|
|
尝 试 应 用 |
|||
|
补 偿 提 高 |
|||
|
达标检测 巩固提升 |
|||
|
作业布置 与 预习提纲 |
|||
|
教 学 札 记 |
本节课主要内容是平行四边形的概念、性质定理并会利用性质定理来解决问题。
|
||
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1