| 上传:admin | 审核发布:admin | 更新时间:2015-3-22 18:11:49 | 点击次数:1600次 |
课案(学生用)
数据的波动(第三课时)
(课型:新授课)
【学习目标】
1.知识与技能
(1)我们要进一步理解方差的概念和计算公式的形成过程.
(2)我们要进一步掌握方差的计算公式并会应用方差比较两组数据波动的大小.
过程与方法
经历方差的应用过程,体会数据波动中方差的求法,积累统计经验,培养我们用统计的知识描述、分析数据,解决实际问题的能力.
情感、态度与价值观
培养我们统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义.
2.中考要求:掌握方差、标准差及其应用,掌握用样本方差估计总体方差.
【学习重难点】
重点:理解极差、方差的概念,掌握其求法.
难点:应用方差对数据波动情况的比较,判断.
【学习过程设计】
课前延伸
一、填空题;
(1)一组数据:![]() ,
,![]() ,0,
,0,![]() ,1的平均数是0,则
,1的平均数是0,则![]() = .方差
= .方差![]() .
.
(2)如果样本方差![]() ,
,
那么这个样本的平均数为 .样本容量为 .
(3)已知![]() 的平均数
的平均数![]() 10,方差
10,方差![]() 3,则
3,则![]() 的平均数为 ,方差为 .
的平均数为 ,方差为 .
二、选择题:
(1)样本方差的作用是( )
A、估计总体的平均水平 B、表示样本的平均水平
C、表示总体的波动大小 D、表示样本的波动大小,从而估计总体的波动大小
(2)一个样本的方差是0,若中位数是![]() ,那么它的平均数是( )
,那么它的平均数是( )
A、等于![]() B、不等于
B、不等于 ![]() C、大于
C、大于 ![]() D、小于
D、小于![]()
(3)已知样本数据101,98,102,100,99,则这个样本的标准差是( )
A、0 B、1 C、![]() D、2
D、2
(4)如果给定数组中每一个数都减去同一非零常数,则数据的( )
A、平均数改变,方差不变 B、平均数改变,方差改变
C、平均数不变,方差不变 A、平均数不变,方差改变
三、甲、乙两台机床生产同种零件,10天出的次品分别是( )
甲:0、1、0、2、2、0、3、1、2、4
乙:2、3、1、2、0、2、1、1、2、1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
课内探究
一、回顾与练习
1、回顾:什么是极差、方差?方差的计算公式是什么?一组数据的方差与这组数据的波动有怎样的关系?
2、分别计算下列两组数据的方差与标准差:
(1)1,2,3,4,5 (2)103 102 98 101 99
二、教师精讲点拨:
例1 下表给出了某市2006年5月28日至6月3日的最高气温,则这些最高气温的极差是___℃.
|
日期 |
5月28日 |
5月29日 |
5月30日 |
5月31日 |
6月1日 |
6月2日 |
6月3日 |
|
最高气温 |
26 |
27 |
30 |
28 |
27 |
29 |
33 |
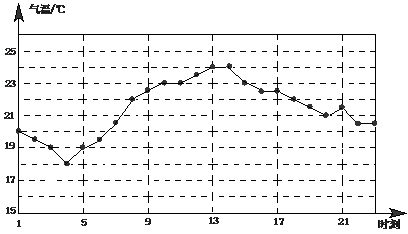
例2 如图是某一天A、B两地的气温变化图.问
(1) 这一天A、B两地的平均气温分别是多少?
(2) A地这一天气温的极差、方差分别是多少?B地呢?
(3) A、B两地的气候各有什么特点?



例3 某校从甲、乙两名优秀选手中选一名选手参加全市中学生运动会跳远比赛.该校预先对这两名选手测试了10次,测试成绩如下表:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
选手甲的成绩(cm) |
585 |
596 |
610 |
598 |
612 |
597 |
604 |
600 |
613 |
601 |
|
选手乙的成绩(cm) |
613 |
618 |
580 |
574 |
618 |
593 |
585 |
590 |
598 |
624 |
(1)他们的平均成绩分别是多少?
(2)甲、乙这10次比赛成绩的方差分别是多少?
(3)这两名运动员的运动成绩各有什么特点?
(4)历届比赛表明,成绩达到596cm就很可能夺冠,你认为为了夺冠应选谁参加这项比赛?
(5)如果历届比赛表明,成绩达到610cm就能打破记录,你认为为了打破记录应选谁参加这项比赛?
三、反馈练习.
1、某校从甲乙两名优秀选手中选一名选手参加全市中学生田径百米比赛(100米记录为12.2秒,通常情况下成绩为12.5秒可获冠军).该校预先对这两名选手测试了8次,测试成绩如下表:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
选手甲的成绩(秒) |
12.1 |
12.4 |
12.8 |
12.5 |
13 |
12.6 |
12.4 |
12.2 |
|
选手乙的成绩(秒) |
12 |
11.9 |
12.8 |
13 |
13.2 |
12.8 |
11.8 |
12.5 |
根据测试成绩,请你运用所学过的统计知识做出判断,派哪一位选手参加比赛更好?为什么?
 2、在某旅游景区上山的一条小路上,有一些断断续续的台阶.图11是其中的甲、乙路段台阶的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
2、在某旅游景区上山的一条小路上,有一些断断续续的台阶.图11是其中的甲、乙路段台阶的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
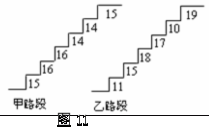
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
五、自我反思
在本节课的学习中,我对方差的大小有什么新的认识?
课后提升
1.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:
|
选 手 |
甲 |
乙 |
丙 |
丁 |
|
平均数(环) |
9.2 |
9.2 |
9.2 |
9.2 |
|
方差(环2) |
0.035 |
0.015 |
0.025 |
0.027 |
则这四人中成绩发挥最稳定的是( )
A.甲 B.乙 C.丙 D.丁
2. 如下图,是某市10月1日至10月7日每天最高、最低气温的折线统计图,在这7天中,日温差最大的一天是( )
 A.10月1日 B.10月2日 C.10月3日 D.10月5日
A.10月1日 B.10月2日 C.10月3日 D.10月5日
3.小明准备买一台电子钟,为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
|
编号 类型 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
|
甲种电子钟 |
1 |
-3 |
-4 |
4 |
2 |
-2 |
2 |
-1 |
-1 |
2 |
|
乙种电子钟 |
4 |
-3 |
-1 |
2 |
-2 |
1 |
-2 |
2 |
-2 |
1 |
(1)分别计算甲、乙两种电子钟走时误差的平均数;
(2)分别计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的钟价格相同,请问:小明买哪种电子钟较好?为什么?
4.某工厂甲、乙两名工人参加操作技能培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
|
甲 |
95 |
82 |
88 |
81 |
93 |
79 |
84 |
78 |
|
乙 |
83 |
92 |
80 |
95 |
90 |
80 |
85 |
75 |
(1)请你计算这两组数据的平均数、中位数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
5.试一试:活动内容:
(1)两人一组,在安静的环境中,一人估计1分钟的时间,另一人记下实际时间,将结果记录下来.
(2)在吵闹的环境中,再做一次这样的试验.
(3)将全班的结果汇总起来并分别计算安静状态和吵闹环境中估计结果的平均值和方差.
(4)两种情况下的结果是否一致?说明理由!
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

