沭阳县蓝天中学初三数学教学案

课    时：总第57课时                    备课：程加林

课    型：新授课                     

教学内容：26．2  二次函数的图象与性质（6）

教学目标：

1．会通过配方求出二次函数的最大或最小值；

2．在实际应用中体会二次函数作为一种数学模型的作用，会利用二次函数的性质求实际问题中的最大或最小值．

教学重点：会通过配方求出二次函数的最大或最小值；

教学难点：在实际应用中体会二次函数作为一种数学模型的作用，会利用二次函数的性质求实际问题中的最大或最小值．

教学过程：

一、 情境创设：

      在实际生活中，我们常常会碰到一些带有“最”字的问题，如问题：某商店将每件进价为80元的某种商品按每件100元出售，一天可销出约100件．该店想通过降低售价、增加销售量的办法来提高利润．经过市场调查，发现这种商品单价每降低1元，其销售量可增加约10件．将这种商品的售价降低多少时，能使销售利润最大？

在这个问题中，设每件商品降价x元，该商品每天的利润为y元，则可得函数关系式为二次函数．那么，此问题可归结为：自变量x为何值时函数y取得最大值？你能解决吗?

[实践与探索]

例1．求下列函数的最大值或最小值．

（1）；        （2）．

分析  由于函数和的自变量x的取值范围是全体实数，所以只要确定它们的图象有最高点或最低点，就可以确定函数有最大值或最小值．

解 ：

 

 

 

 

 

 

 

回顾与反思  最大值或最小值的求法，第一步确定a的符号，a＞0有最小值，

a＜0有最大值；第二步配方求顶点，顶点的纵坐标即为对应的最大值或最小值．

探索  试一试，当2．5≤x≤3．5时，求二次函数的最大值或最小值．

 

 

 

 

例2．某产品每件成本是120元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间关系如下表：

x（元）	130	150	165
y（件）	70	50	35

若日销售量y是销售价x的一次函数，要获得最大销售利润，每件产品的销售价定为多少元？此时每日销售利润是多少？

分析  日销售利润=日销售量×每件产品的利润，因此主要是正确表示出这两个量．

解 ： 

 

 

 

 

 

 

 

 

 

例3．如图26．2．8，在Rt⊿ABC中，∠C=90°，BC=4，AC=8，点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF，设DE=x，DF=y．

（1）用含y的代数式表示AE；

（2）求y与x之间的函数关系式，并求出x的取值范围；

（3）设四边形DECF的面积为S，求S与x之间的函数关系，    并求出S的最大值．

解 ： 

 

 

 

 

 

 

 

 

 

 [当堂课内练习]

1．对于二次函数，当x=      时，y有最小值．

2．已知二次函数有最小值 –1，则a与b之间的大小关系是      （   ）

A．a＜b        B．a=b      C．a＞b     D．不能确定

3．某商场销售一批衬衫，平均每天可售出20件，每件盈利40件，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经过市场调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．

（1）若商场平均每天要盈利1200元，每件衬衫应降价多少元？

（2）每件衬衫降价多少元时，商场平均每天盈利最多？

 

 

 

 

 

[本课课外作业]

A组

1．求下列函数的最大值或最小值．

（1）；        （2）．

 

 

2．已知二次函数的最小值为1，求m的值．，

 

 

 

 

3．心理学家发现，学生对概念的接受能力y与提出概念所用的时间x（单位：分）之间满足函数关系：．y值越大，表示接受能力越强．

（1）x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？

（2）第10分时，学生的接受能力是多少？

（3）第几分时，学生的接受能力最强？

 

 

 

 

B组

4．不论自变量x取什么数，二次函数的函数值总是正值，求m的取值范围．

 

 

 

 

 

 

5．如图，有长为24m的篱笆，一面利用墙（墙的最大可用长度a为10m），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x m，面积为S m2．

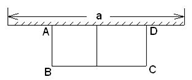（1）求S与x的函数关系式；

（2）如果要围成面积为45 m2的花圃，AB的长是多少米？

（3）能围成面积比45 m2更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．

 

 

 

 

 

 

 

 

 

6．如图，矩形ABCD中，AB=3，BC=4，线段EF在对角线AC上，EG⊥AD，FH⊥BC，垂足分别是G、H，且EG+FH=EF．

（1）求线段EF的长；

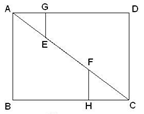（2）设EG=x，⊿AGE与⊿CFH的面积和为S，

写出S关于x的函数关系式及自变量x的取值范围，

并求出S的最小值．