| 上传:admin | 审核发布:admin | 更新时间:2015-3-23 15:38:25 | 点击次数:709次 |
课题 27.2.1 相似三角形的判定3 学案 人教版九年级下
导学目标知识点:初步掌握“三组对应边的比相等的两个三角形相似”的判定方法,以及“两组对应边的比相等且它们的夹角相等的两个三角形相似”的判定方法;能够运用三角形相似的条件解决简单的问题.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
两个三角形全等有哪些判定方法?我们学习过哪些判定三角形相似的方法?
二、合作探究(课堂导学)
实验探究1:任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长是的![]() 倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同学交流一下,看看是否有同样的结论。
倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?与同学交流一下,看看是否有同样的结论。
探求证明方法.
如图,在![]() 和
和![]() 中,
中,![]() ,求证
,求证![]() ∽
∽![]() 证明 :
证明 :
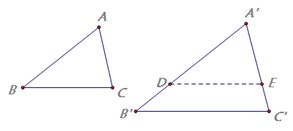
归纳
三角形相似的判定方法1
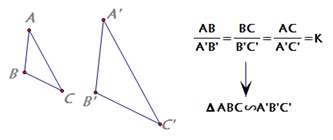
实验探究2:可否用类似于判定三角形全等的SAS方法,能否通过两个三角形的两组对应边的比相等和它们对应的夹角相等,来判定两个三角形相似呢?
(画图,自主展开探究活动)
归纳
三角形相似的判定方法2
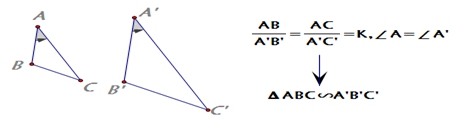
例1 根据下列条件,判断![]() 与
与![]() 是否相似,并说明理由:
是否相似,并说明理由:
(1)![]()
(2)![]()
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
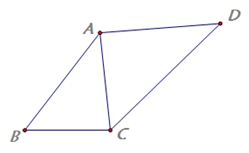 已知:如图,在四边形ABCD中,
已知:如图,在四边形ABCD中,![]() ,AB=6,BC=4,AC=5,CD=
,AB=6,BC=4,AC=5,CD=![]() ,求AD的长.
,求AD的长.
提示:由已知一对对应角相等及四条边长,猜想应用“两组对应边的比相等且它们的夹角相等”来证明.计算得出![]() ,结合
,结合![]() ,证明
,证明![]() ,再利用相似三角形的定义得出关于AD的比例式
,再利用相似三角形的定义得出关于AD的比例式![]() ,从而求出AD的长.
,从而求出AD的长.
拓展延伸(课外练习):
1如果在![]() 中
中![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,这两个三角形一定相似吗?试着画一画、看一看?
,这两个三角形一定相似吗?试着画一画、看一看?
2.如图,![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,求证:
的中点,求证:![]() .
.
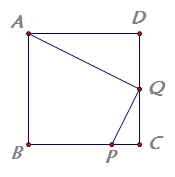
3.如图,P为正方形ABCD边BC上的点,且BP=3PC,Q为DC的中点,
求证:![]()
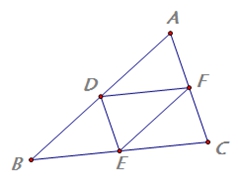
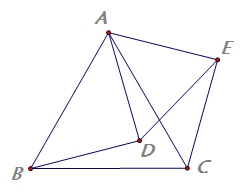 4.如图,
4.如图,![]() ,求证:
,求证:![]()
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

