| 上传:admin | 审核发布:admin | 更新时间:2015-3-23 18:51:16 | 点击次数:644次 |
|
教学时间 |
|
课题 |
解直三角形应用(三) |
课型 |
新授课 |
||||||||||
|
教 学 目 标 |
知 识 和 能 力 |
使学生会把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决. |
|||||||||||||
|
过 程 和 方 法 |
逐步培养学生分析问题、解决问题的能力. |
||||||||||||||
|
情 感 态 度 价值观 |
渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识.
|
||||||||||||||
|
教学重点 |
要求学生善于将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决. |
||||||||||||||
|
教学难点 |
要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而利用所学知识把实际问题解决. |
||||||||||||||
|
教学准备 |
教师 |
多媒体课件 |
学生 |
“五个一” |
|||||||||||
|
课 堂 教 学 程 序 设 计 |
设计意图 |
||||||||||||||
|
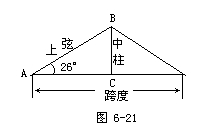
1.导入新课 上节课我们解决的实际问题是应用正弦及余弦解直角三角形,在实际问题中有时还经常应用正切和余切来解直角三角形,从而使问题得到解决. 2.例题分析 例1.如图6-21,厂房屋顶人字架(等腰三角形)的跨度为10米,∠A-26°,
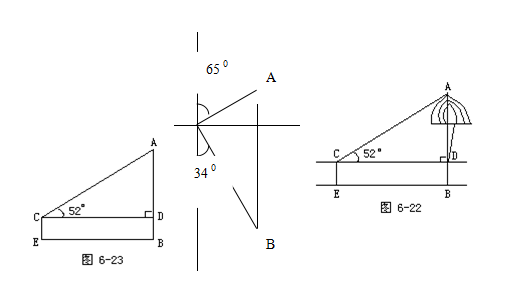
分析:上图是本题的示意图,同学们对照图形,根据题意思考题目中的每句话对应图中的哪个角或边,本题已知什么,求什么? 由题意知,△ABC为直角三角形,∠ACB=90°,∠A=26°,AC=5米,可利用解Rt△ABC的方法求出BC和AB. 学生在把实际问题转化为数学问题后,大部分学生可自行完成 例题小结:求出中柱BC的长为2.44米后,我们也可以利用正弦计算上弦AB的长。 如果在引导学生讨论后小结,效果会更好,不仅使学生掌握选何关系式,更重要的是知道为什么选这个关系式,以培养学生分析问题、解决问题的能力及计算能力,形成良好的学习习惯. 另外,本题是把解等腰三角形的问题转化为直角三角形的问题,渗透了转化的数学思想. 例2.如图,一艘海轮位于灯塔P的北偏东65 . 引导学生根据示意图,说明本题已知什么,求什么,利用哪个三角形来求解,用正弦、余弦、正切、余切中的哪一种解较为简便?
3巩固练习
为测量松树AB的高度,一个人站在距松树15米的E处,测得仰角∠ACD=52°,已知人的高度是1.72米,求树高(精确到0.01米).
首先请学生结合题意画几何图形,并把实际问题转化为数学问题. Rt△ACD中,∠D=Rt∠,∠ACD=52°,CD=BE=15米,CE=DB=1.72米,求AB?
(三)总结与扩展
请学生总结:通过学习两个例题,初步学会把一些实际问题转化为数学问题,通过解直角三角形来解决,具体说,本节课通过让学生把实际问题转化为数学问题,利用正切或余切解直角三角形,从而把问题解决. 本课涉及到一种重要教学思想:转化思想. |
|
||||||||||||||
|
作业 设计 |
必做 |
教科书P92:5 |
|||||||||||||
|
选做 |
教科书P92:6 |
||||||||||||||
|
教 学 反 思 |
|
||||||||||||||
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1