| 上传:admin | 审核发布:admin | 更新时间:2015-3-29 10:29:50 | 点击次数:762次 |
2.2直线与平面的平行与垂直的判定及其性质
高考要求:
理解空间中线面平行、垂直的有关性质与判定定理.
理解以下判定定理.
l 如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
l 如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
理解以下性质定理,并能够证明.
l 如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.
l 垂直于同一个平面的两条直线平行.
能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.
能根据定义解决两条异面直线所成的角、直线和平面所成的角、简单计算问题.
教学目标:
1.以立体几何的定义、公理和定理为出发点,通过直观感知、操作确认、思辨论证,认识和理解空间中线面平行、垂直的判定定理
2.认识和理解空间中线面平行以及垂直的性质定理,灵活运用判定定理和性质定理
3.掌握转化思想 线线平行![]() 线面平行 线线垂直
线面平行 线线垂直![]() 线面垂直
线面垂直
教学重点:通过直观感知、操作确认,归纳出判定定理和性质定理
教学难点:性质定理的证明
第4,5课时
课前导学:
(一)直线与平面平行的判定与性质
(1)线面平行的判定定理:
如果平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。
符号表示:
定理说明:证明线面平行的关键在于证明线线平行,简述为:线线平行![]() 线面平行
线面平行
(2)线面平行的性质定理:
如果一条直线与一个平面平行,则过这条直线的任意一个平面与此平面的交线与该直线平行。
符号表示:
定理证明:
定理说明:线面平行的性质定理又可以作为线线平行的判定定理,
简述为:线面平行![]() 线线平行
线线平行
由判定及其性质可知 线面平行![]() 线线平行
线线平行
预习自测:
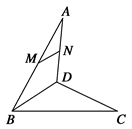
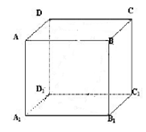
1.如图,在空间四边形ABCD中,若M、N为AB、AD的中点,求证: MN∥平面BDC.
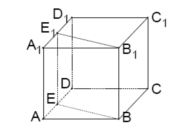
2.经过正方体ABCD-A1B1C1D1的棱BB1作一平面交平面
AA1D1D于E1E,求证:E1E∥B1B
典型例题:
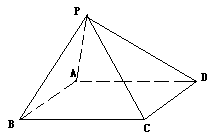
例1.已知P是平行四边形ABCD所在平面外一点,E、F分别为AB、PD的中点,求证:
AF∥平面PEC
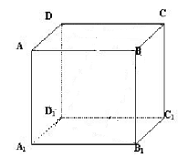
例2.在正方体ABCD-A1B1C1D1中,E、F分别为棱BC、C1D1的中点. 求证:EF∥平面BB1D1D.
例3.已知![]() 、
、![]() 、
、![]() 、
、![]() 分别是四面体
分别是四面体![]()
![]() 的棱
的棱![]() 、
、![]() 、
、![]() 、
、![]() 的中点,
的中点,
求证:![]() ∥平
∥平![]() 面
面![]() .
.
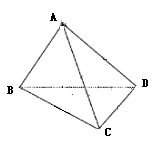
例4.如右图,平行四边形EFGH的顶点分别在空间四边形ABCD各边上,
 求证:BD//平面EFGH.
求证:BD//平面EFGH.
例5.已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.
第6,7课时
课前导学:
(二)直线与平面垂直的判定与性质
(1)直线与平面垂直定义:
如果一条直线和平面内任何一条直线都垂直,称这条直线和这个平面垂直,记作:
其中,直线叫做这个平面的垂线,平面叫做这条直线的垂面,交点叫垂足
画法:画直线和平面垂直时,通常要把直线画成和表示平面的平行四边形的一边垂直。
注:①直线与平面垂直是直线与平面相交的一种特殊情况
②定义中“任何”表示所有,不能理解为“无数”。若直线与平面内的无数条
直线垂直,则直线不一定垂直于平面;
③ ![]() ⊥
⊥![]() 等价于对任意的直线
等价于对任意的直线![]() Ì
Ì![]() ,都有
,都有![]() ⊥
⊥![]() 。
。
(2)直线与平面垂直的判定定理:
如果一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
符号表示:
定理说明:证明线面垂直的关键在于证明两个线线垂直,简述为:线线垂直![]() 线面垂直
线面垂直
注:(1) 定理中“两条相交直线”二字不可忽视,否则线面垂直的结论不成立
(2)证明线面垂直归结为证明线线垂直,证明无数多线线垂直减弱为只需证明两个线线垂直即可 简述为:线线垂直![]() 线面垂直
线面垂直
(3)直线和平面所成的角:
一条直线PA和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,
交点叫做斜足
过斜线上斜足以外的一点向平面引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角
(4)线面垂直的性质定理:
垂直于同一个平面的两条直线平行
符号表示:
典型例题:
例1.已知:a∥b,![]() ,求证:
,求证:![]()
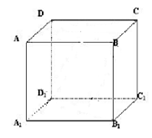
例2.在正方体ABCD-A1B1C1D1,上下底面对角线分别交于![]() ,(1)求证:
,(1)求证:![]() 平面ABCD
平面ABCD
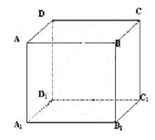 (2)求证:
(2)求证:![]() 平面
平面![]()
(3)E是![]() 的中点,求证:
的中点,求证:![]()
![]() 平面BED
平面BED
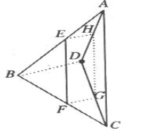
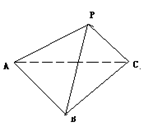
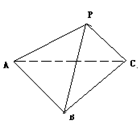
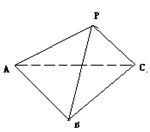
例3. 三棱锥![]() 中,若已知
中,若已知
(1) PA、PB、PC两两垂直,且H是![]() 的垂心,求证:
的垂心,求证:![]() 平面ABC
平面ABC
(2) ![]() ,求证:
,求证:![]()
(3) O是![]() 的外心,若PA=PB=PC,求证:
的外心,若PA=PB=PC,求证:![]() 平面ABC
平面ABC
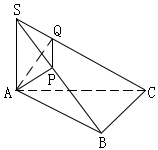 例4.ΔABC中,已知∠ABC=900,SA⊥ΔABC所在平面,又点A在SB和SC上的射影分别是P、Q,求证:PQ⊥SC
例4.ΔABC中,已知∠ABC=900,SA⊥ΔABC所在平面,又点A在SB和SC上的射影分别是P、Q,求证:PQ⊥SC
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

