3.3 直线的交点坐标与距离公式

一、教学目标：

1会用解方程组的方法求两条相交直线的交点坐标

2掌握两点间距离公式并会应用.

3学习并领会寻找点到直线距离公式的思维过程以及推导方法.

4掌握点到直线的距离公式与两平行线间的距离公式，并能熟练运用公式.

教学重点：判断两直线是否相交，求交点坐标；点到直线的距离公式

教学难点：推导两点间距离公式

二、预习导学

（一） 知识梳理

1、两条直线的交点坐标

直线

一般地，将两条直线的方程组联立，得到方程组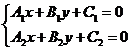

若方程组有         ，则两条直线             ，此解就是交点的坐标；若方程组无解，则两条直线           ，此时两条直线           。

2.两点间的距离公式：设是平面直角坐标系中的任意两个点，则=             

3.点到直线的距离为：               

4. 已知两条平行线直线 ：，：，则与的距离                                

d=                       

（二）预习交流

求经过两条直线2＋－８＝0和－2＋1＝0的交点，且平行于直线４－3-7＝0的直线方程.

三、问题引领，知识探究

问题1：已知两直线相交，如何求这两直线交点的坐标？

 

练习内化1：判断下列两条直线的位置关系

(1)  直线:与直线:

(2)  直线:与直线:

(3)  直线:与直线:

 

 

 

 

变式1：求满足下列条件的直线方程。

(1) 经过两直线2x-3y+10=0与3x+4y-2=0的交点，且过点(1,0)的直线

(2) 经过两直线2x-3y+10=0与3x+4y-2=0的交点，且和直线3x-2y+4=0垂直.

 

 

 

 

 

问题2：已知平面上两点，如何求的距离？

 

 

练习内化2：已知点P1(2，-1)和P2(-3，2)，求｜P1P2｜

 

变式2：已知点A(-1,2) 和B(2,) , 在x轴上求一点P，使|PA|=|PB|，

并求|PA|的值.

 

 

问题3：已知点，直线,如何求点P到直线l的距离？

 

练习内化3：求点到直线的距离

 

 

 

变式3：已知点，求的面积.

 

 

 

 

 

 

四、目标检测

1.求经过两条直线的交点且垂直于直线的直线方程。

 

 

 

 

2.求点到下列直线的距离.

(1)；(2) 

 

3.求两平行线：，：的距离.

 

五、分层配餐

A组题

1.已知直线经过点（2，3）且经过两条直线的交点，求该直线的方程。

 

 

2.求下列点到直线的距离：

(1)A（－2，3），3＋４＋3＝0； (2)C（1，－2），４＋3＝0.

 

 

 

3.求下列两条平行线的距离：

(1)2＋3－８＝0，2＋3＋1８＝0，

(2)3＋４＝10，3＋４＝0.

 

 

 

B组题

4.求点P(－5，7）到直线12＋5－3＝0的距离.

 

 

 

5.已知点A（，6）到直线3－４＝2的距离d取下列各值，求的值：

(1)d＝４，（2）d＞４

 

 

 

6. 直线＋2＋８＝0，4＋3＝10和2－＝10相交于一点，求的值.

 

 

 

C组题

7.直线的交点在第四象限，求的取值范围。