| 上传:admin | 审核发布:admin | 更新时间:2015-3-30 9:17:33 | 点击次数:780次 |
湖南省怀化市湖天中学高中数学 1.1 正弦定理和余弦定理学案 新人教A版必修5
![]() 学习目标
学习目标
1. 进一步熟悉正、余弦定理内容;
2. 掌握在已知三角形的两边及其中一边的对角解三角形时,有两解或一解或无解等情形.
![]() 学习重难点
学习重难点
1. 重点:正、余弦定理内容
2. 难点:已知三角形的两边及其中一边的对角解三角形时的讨论
一、知识链接
问题1:在解三角形时,已知三边求角,用 定理;
已知两![]() 边和夹角,求第三边,用 定理;已知两角和一边,用 定理.
边和夹角,求第三边,用 定理;已知两角和一边,用 定理.
问题2:在△ABC中,已知 A=![]() ,a=25
,a=25![]() ,b=50
,b=50![]() ,解此三角
,解此三角![]() 形.
形.
二、试一试
探究1:在△ABC中,已知下列条件,解三![]() 角形.
角形.
① A=![]() ,a=25,b=50
,a=25,b=50![]() ;② A=
;② A=![]() ,a=
,a=![]() ,b=50
,b=50![]() ;③ A=
;③ A=![]() ,a=50,b=50
,a=50,b=50![]() .
.
![]()
思考:解的个数情况为何会发生变化?
探究2:用如下图示分析解的情况(A为锐角时).
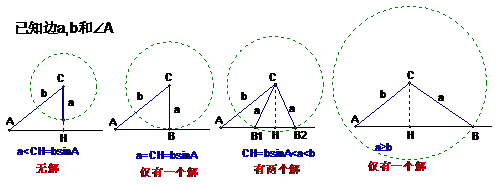
试试:
1. 用图示分析(A为直角时)解的情况? 2.用图示分析(A为钝角时)解的情![]() 况?
况?
※ 模仿练习
例1. 在![]() ABC中
ABC中![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,试判断此三角形的解的情况.
,试判断此三角形的解的情况.
变式:在![]() ABC中,若
ABC中,若![]() ,
,![]() ,
,![]() ,则符合题意的b的值有_____个
,则符合题意的b的值有_____个![]() .
.![]()
例2. 在![]() ABC中,
ABC中,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
变式:在![]() ABC中,若
ABC中,若![]() ,
,![]() ,且
,且![]() ,求角C.
,求角C.
三、总结提升
※ 学习小结
1. 已知三角形两边及其夹角(用余弦定理解决);
2. 已知三角形![]() 三边问题(用余弦定理解决);
三边问题(用余弦定理解决);
3. 已知三角形两角和一![]() 边问题(用正弦定理解决);
边问题(用正弦定理解决);
4. 已知三角形两边和其中一边的对角问题(既可用正弦定理,也可用余弦定理,可能有一解、
两解和无解三种情况).
※ 知识拓展
在![]() ABC中,已知
ABC中,已知![]() ,讨论三角形解的情况 :
,讨论三角形解的情况 :
①当A为钝角或直角时,必须![]() 才能有且只有一解;否则无解;
才能有且只有一解;否则无解;
②当A为锐角时,如果![]() ≥
≥![]() ,那么只有一解;
,那么只有一解;
如果![]() ,那么可以分下面三种情况来讨论:
,那么可以分下面三种情况来讨论:![]()
(1)若![]() ,则有两解;(2)若
,则有两解;(2)若![]() ,则只有一解;(3)若
,则只有一解;(3)若![]() ,则无解.
,则无解.
![]() 当堂检测
当堂检测
1. 已知a、b为△A![]() BC的边,A、B分别是a、b的对角,且
BC的边,A、B分别是a、b的对角,且![]() ,则
,则![]() 的值=( ).
的值=( ).
A. ![]() B.
B. ![]() C.
C. ![]()
![]() D.
D. ![]()
2. 已知在△ABC中,sinA∶sinB∶sinC=3∶5∶7,那么这个三角形的最大角是( ).
A.135° B.90° C.120° D.150°
3. 如果将直角三角形三边增加同样的长度,则新三角形形状为( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.由增加长度决定
4. 在△ABC中,sinA:sinB:sinC=4:5:6,则cosB= .
5. 已知![]() △ABC中,
△ABC中,![]() ,试判断△ABC的形状 .
,试判断△ABC的形状 .
![]() 课后作业
课后作业
1. 在![]() ABC中,
ABC中,![]() ,
,![]() ,
,![]() ,如果利用正弦定理解三角形有两解,求x的取值范围.
,如果利用正弦定理解三角形有两解,求x的取值范围.
2. 在![]() ABC中,
ABC中,![]() 其三边分别为a、b、c,且满足
其三边分别为a、b、c,且满足![]() ,求角C.
,求角C.
![]() 课后反思
课后反思
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

