河北省石家庄市第一中学高中数学 3.1不等关系与不等式（1）教案 新人教A版必修5

　　　　　　　　　　　　　

教学目标：

1．知识与技能：

通过具体情景，感受在现实世界和日常生活中存在着大量不等关系，理解不等式（组）的实际背景，掌握不等式的基本性质，会用不等式的性质证明简单的不等式．

2．过程与方法：

通过解决具体问题，学会依据具体问题的实际背景分析问题、解决问题的方法．

3．情感、态度与价值观：

通过解决具体问题，体会数学在生活中的重要作用，培养严谨的思维习惯．

重　  点：理解不等式（组）对于刻画不等关系的意义和价值；掌握不等式的性质和利用不等式的性质证明简单的不等式．

难　  点：利用不等式的性质证明简单的不等式．

教学过程：

一、不等关系

在现实世界和日常生活中，既有相等关系，又存在着大量的不等关系．如两点之间线段最短，三角形两边之和大于第三边，等等．人们还经常用长与短、高与矮、轻与重、胖与瘦、大与小、不超过或不少于等来描述某种客观事物在数量上存在的不等关系．在数学中，我们用不等式来表示不等关系．

下面我们首先来看如何利用不等式来表示不等关系．

问题1：设点A与平面的距离为d，B为平面上的任意一点，则d≤．

问题2：某种杂志原以每本2.5元的价格销售，可以售出8万本．根据市场调查，若单价每提高0.1元，销售量就可能相应减少2000本．若把提价后杂志的定价设为x元，怎样用不等式表示销售的总收入仍不低于20万元？

分析：若杂志的定价为x元，则销售的总收入为万元．那么不等关系“销售的总收入不低于20万元”可以表示为不等式≥20

问题3：某钢铁厂要把长度为4000mm的钢管截成500mm和600mm两种，按照生产的要求，600mm钢管的数量不能超过500mm钢管的3倍．怎样写出满足上述所有不等关系的不等式呢？

分析：假设截得500mm的钢管x根，截得600mm的钢管y根..

根据题意，应有如下的不等关系：

（1）解得两种钢管的总长度不能超过4000mm；

（2）截得600mm钢管的数量不能超过500mm钢管数量的3倍；

（3）解得两钟钢管的数量都不能为负．

由以上不等关系，可得不等式组：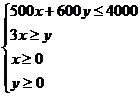

二、数运算性质与大小顺序之间的关系

；

；

．

 

三、 不等式的性质

定理1：（对称性）如果a>b，那么b<a；如果b<a，那么a>b；即  a>bb<a．

证明： 

说明：把不等式的左边和右边交换，所得不等式与原不等式异向．

定理2：（传递性）如果a>b，b>c，那么a>c． 即  a>b，b>ca>c．

证明：

说明：由定理1，可知定理2还可以表示为：．

定理3：（加法保序性）若a>b，则a+c>b+c，即a>ba+c>b+c．

证明： 

推论1：（移项法则）不等式中任何一项的符号变成相反的符号后，可以把它从一边移到另一边．

推论2：（加法法则）a>b，c>da+c>b+d．

证明： 

推广：两个或几个同向不等式两边分别相加，所得不等式与原不等式同向．

定理4：（乘法保序性）若a>b，c>0，则ac>bc；若a>b，c<0，则ac<bc．即

　　　　a>b，c>0ac>bc；a>b，c<0ac<bd．

证明： 

推论1：（乘法法则）a>b>0，c>d>0ac>bc．

证明： 

推广：两个或几个两边都是正数的同向不等式两边分别相乘，所得不等式与原不等式同向．

推论2：（乘方法则）a>b>0(nN,且n>1) 

定理5：（开方法则）若 则(． 即

    

证明：

练习：课本：P74．

小结：1．不等式的性质是进行不等式的证明和解不等式的依据．

2．在运用不等式的性质时，一定要严格掌握它们成立的条件．

四、应用举例

例1．已知，求证．

证明：

例2．已知，求证：．

证明：

例3．已知，求证．

证明：．，

故   ．

例4．设，求的取值范围．

解：由；

，且，．

    由．

例5．设，且．求的取值范围．

解：．

设，

即．

．．

由得，．

．

小结：1．应用不等式的性质证明不等式，一般是从已知的不等式出发，应用不等式的性质进行变形，直至变换出所要证的不等式．

2．根据不等式的性质，同向不等式可以相加，同向且两边均为正数的不等式可以相乘；同向不等式不能相减和相除，异向不等式的相减或相除应转化继同向不等式后用相加或相乘来进行．

3．同号两数的顺序关系与其倒数的顺序相反．

4．用不等式的性质求变量的范围时，是通过同向不等式相加或相乘来完成的，如果是有等号的还应注意两端能否取得等号．

五、课堂练习： 

六、作业： 

七、补充题：

1．设a<b<0，下列命题：①；②；③；④中，假命题的个数是（    ）

   (A) 3          (B) 2          (C) 1           (D)0           答：选 (C)．

2．若a,b是任意实数，且a>b，四个不等式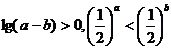，中，能成立的不等式的个数是（    ）

（A）1  　（B）2 　 （C）3    　（D）4  　   答：选（A）．