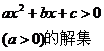| 上传:admin | 审核发布:admin | 更新时间:2015-3-30 11:13:42 | 点击次数:760次 |
3.2 一元二次不等式及其解法
第1课时
学习目标
1.理解一元二次方程、一元二次不等式与一元二次函数之间的关系;
2.掌握图象法解一元二次不等式的方法。
3.掌握含有字母系数的不等式的解法。
要点精讲
1.设相应的一元二次方程![]() 的两根为
的两根为![]() ,
,
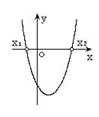
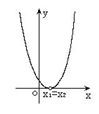
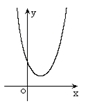
![]() ,不等式的解的各种情况如下表:
,不等式的解的各种情况如下表:
|
|
|
|
|
|
二次函数
(
|
|
|
|
|
一元二次方程
|
有两相异实根
|
有两相等实根
|
无实根 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 时,不等式两边同乘以
时,不等式两边同乘以![]() ,转化为二次项系数为正的标准一元二次不等式
,转化为二次项系数为正的标准一元二次不等式
2.若![]() 的解集是
的解集是![]() ,则
,则![]() 或
或![]()
3.若![]() 的解集是
的解集是![]() ,则
,则![]() 或
或![]()
范例分析
例1.(1)不等式![]() 的解集是 ;
的解集是 ;
(2)不等式![]() 的解集是 ;
的解集是 ;
(3)不等式![]() 的解集是 ;
的解集是 ;
(4)不等式![]() 的解集是 ;
的解集是 ;
例2.已知关于![]() 的不等式
的不等式![]()
⑴若不等式的解集为![]() ,求实数
,求实数![]() 的值;
的值;
⑵若不等式的解集为![]() ,求实数
,求实数![]() 的值;
的值;
⑶若不等式的解集为R,求实数![]()
![]() 的取值范围;
的取值范围;
(4)若不等式的解集为![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
例3.解关于![]() 的不等式:
的不等式:
![]()
![]()
例4. 解关于![]() 的不等式:
的不等式:![]() 。
。
规律总结
1.解一元二次不等式的步骤
(1)判号:检查二次项系数![]() 是否为正,若为负值,则利用不等式性质转化为正值;
是否为正,若为负值,则利用不等式性质转化为正值;
(2)求根:计算判![]() 别式
别式![]() ,求出相应方程的实数根;
,求出相应方程的实数根;
(3)标根:在数轴上标出所得的实数根(注意两实数根的大小顺序,特别是当实数根中含有字母系数时),并画出开口向上的抛物线的示意图;
(4)写解集:根据示意图及其一元二次不等式的几何意义,写出解集。
2.当一元二次不等式的二次项系数含有字母系数时,不能忽略二次项系数为零的特殊情形。
3.不等式的解要写成解集的形式,即用集合或区间表示。
基础训练
一、选择题
1.在下列不等式中,解集为![]() 的是( )
的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.集合![]() ,
,![]() ,则
,则![]() 的子集有( )
的子集有( )
A.15个 B.16个 C.7个 D.8个
3.若不等式![]() 的解集是
的解集是![]() ,则
,则![]() ( )
( )
(A)![]() (B)14 (C)
(B)14 (C)![]() (D)10
(D)10
4.若关于![]() 的不等式
的不等式![]() 的解是
的解是![]() 或
或![]() ,
,
则关于![]() 的不等式
的不等式![]() 的解是( )
的解是( )
(A)![]() 或
或![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() 或
或![]()
5.设![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集是( )
的解集是( )
(A)![]() 或
或![]() (B)
(B)![]() (C)
(C)![]() 或
或![]() (D)
(D)![]()
二、填空题
6.若![]() 有负值,则
有负值,则![]() 的取值范围是________。
的取值范围是________。
7.在R上定义运算![]() :
:![]() ,则不等式
,则不等式![]() 的解集为_______
的解集为_______
8.不等式![]() 的解集是
的解集是![]() ,对于系数
,对于系数![]() 、
、![]() 、
、![]() 有下列结论
有下列结论
(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() (5)
(5)![]() >0,
>0,
其中正确结论的序号是___________.
三、解答题
9.解下列不等式:
(1)x2-7x+12>0; (2)-x2-2x+3≥0;![]()
(3)x2-2x+1<0 ; (4)x2-2x+2![]() <0。
<0。
10.设![]() ,解关于
,解关于![]() 的不等式
的不等式![]() 。
。
四、能力提高
11.设k∈R , x1 , x2是方程x2-2kx+1-k2=0的两个实数根, 则x![]() +x
+x![]() 的最小值为( C )
的最小值为( C )
A. —2 B. 0 C. 1 D. 2
12.解不等式:![]() 。
。
3.2 一元二次不等式及其解法第1课时参考答案
例1.(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 。
。
例2.(1)![]() 是方程
是方程![]() 的两个实根,且
的两个实根,且![]() ,得
,得![]() ;
;
(2)![]() 且
且![]() ,得
,得![]() ;
;
(3)![]() 且
且![]() ,得
,得![]() ;
;
(4)![]() 且
且![]() ,得
,得![]() 。
。
例3.解:![]()
因为![]()
![]() ,对参数
,对参数![]() 进行分类讨论:
进行分类讨论:
①若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
②若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
③若![]() 或
或![]() ,则
,则![]() ,不等式的解集为
,不等式的解集为![]() ;
;
④若![]() ,则
,则![]() ,不等式的解集为
,不等式的解集为![]() ;
;
(2)①若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
②若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
③若![]() 则不等式的解集为
则不等式的解集为![]() ;
;
评注:若对参数进行分类讨论,其结果应对参数分类叙述,不可将各类结果求并集,为了表述简洁明了,可把其解的结构一样的相同参数合在一起。
例4.解:![]()
(1)当![]() ,即
,即![]() 或
或![]() 时,不等式的解集为
时,不等式的解集为
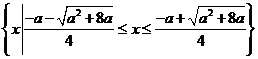 ;
;
(2)当![]() ,即
,即![]() 或
或![]() 时,不等式的解集为
时,不等式的解集为![]() ;
;
(3)当![]() ,即
,即![]() 时,不等式的解集为
时,不等式的解集为![]() 。
。
参考答案
1~5 DBCCA
6.![]() 或
或![]() ;提示:
;提示:![]() 。
。
7.![]()
8.(3)(5);提示:![]() 。
。
9.答案:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 。
。
10.解:移项整理得![]() ,因为
,因为![]() ,所以
,所以![]() 。
。
11.C;
10.解:![]() ,
,
①若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
②若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
③若![]() ,则不等式的解集为
,则不等式的解集为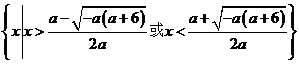 。
。
3.2 一元二次不等式及其解法
第2课时
学习目标
1.掌握同![]() 解不等式之间的转化;
解不等式之间的转化;
2.熟悉并掌握用数轴标根法解高次不等式;
3.掌握指数不等式与对数不等式的同解变形![]()
要点精讲
1![]() 同解不等式:两个不等式如果解集相等,那么这两个不等式就叫做同解不等式
同解不等式:两个不等式如果解集相等,那么这两个不等式就叫做同解不等式![]()
2![]() 同解变形:一个不等式变形为另一个不等式时,如果这两个不等式是同解不等式,那
同解变形:一个不等式变形为另一个不等式时,如果这两个不等式是同解不等式,那
么这种变形就叫做同解变形![]()
过去我们学过的一元一次不等式解法,如去分母、去括号、移项、合并同类项等等,都是同解变形,因此最后得到的解(不等式)就是原不等式的解![]() 解指数不等式与对数不等式的实质是利用同解变形进行转化。
解指数不等式与对数不等式的实质是利用同解变形进行转化。
3.(1)![]() >0
>0![]() f(x)g(x)>0;(2)
f(x)g(x)>0;(2)![]() <0
<0![]() f(x)g(x)<0;
f(x)g(x)<0;
(3)![]() ≥0
≥0![]()
![]() ;(4)
;(4)![]() ≤0
≤0![]()
![]()
4.简单的一元高次不等式:先因式分解,再采用“数轴标根法”。如:
把不等式化为(x–x1)(x–x2)(x–x3)(x–x4)>0(其中x1<x2<x3<x4),再从右往左,从上往下画曲线。
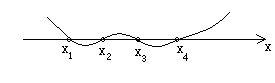
所以不等式的解集为![]() .
.
5. 一元分式不等式:采用“数轴标根法”.
步骤:移项、通分、(![]() 化整式)、求解。
化整式)、求解。
评注:(1)“数轴标根法”的本质是考虑各因式的符号,对于偶次因式,要单独考虑此因式的值能否为零,而奇次因式的符号与一次因式的符号是相同的;(2)如果不等式的一端非零,那么先移项进行因式分解,再判断符号,因式分解要彻底。
范例分析
例1.解下列不等式
(I)![]() ;
;
(II) ![]() 。
。
例2.解下列不等式
(1)![]() <0;(2)
<0;(2)![]() >1。
>1。
例3.解不等式(1)![]() ;(2)
;(2)![]()
![]()
例4.设![]() (
(![]() 为实常数),且方程
为实常数),且方程![]() 有两个实数根为
有两个实数根为![]() ,
,![]() ,
,
(![]() 1)求函数
1)求函数![]() 的解析式.(2)
的解析式.(2)![]() 设
设![]() ,解关于
,解关于![]() 的不等式
的不等式![]() .
.
规律总结
1.一元一次不等式和一元二次不等式的解法是解各类不等式的基础,要予以高度重视![]() 尤其把握好解一元二次不等式的解题步骤:一是将二次项系数变为正的;二是确定不等式对应方程根的情况(由判别式来确定);三是结合图象(二次函数图象)写出不等式的解集
尤其把握好解一元二次不等式的解题步骤:一是将二次项系数变为正的;二是确定不等式对应方程根的情况(由判别式来确定);三是结合图象(二次函数图象)写出不等式的解集![]()
2.解高次不等式的方法步骤:
方法:序轴标根法.
步骤:①化一边为零且让最高次数系数为正;②把根标在数轴上;③右上方向起画曲线,让曲线依次穿过标在数轴上的各个根;④根据“大于0在上方,小于0在下方”写出解集。
注:①重根问题处理方法:“奇过偶不过”.②分式不等式转化为高次不等式求解.
3.一些特殊不等式的求解,转化是一方面,借助于函数的性质和图象也是解决问题的有效手段。
基础训练
一、选择题
1.不等式![]() 的解集是( )
的解集是( )
A. ![]() B.
B.![]()
C.![]() D.
D.![]()
2.不等式![]() 的解集是 ( )
的解集是 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3.不等式![]() ≥1的解集为 ( )
≥1的解集为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知不等式![]() 对任何实数
对任何实数![]() 恒成立,则不等式
恒成立,则不等式![]() 的
的
解集是 ( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.函数![]() 和
和![]() 的定义域是
的定义域是![]() ,且
,且![]() 的解集为
的解集为![]() ,
,![]() 的解集为
的解集为![]() ,则
,则![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
6.不等式![]() 的解集是 。
的解集是 。
7.不等式![]() 的解集是
的解集是
8.不等式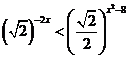 的解集是____ _.
的解集是____ _.
三、解答题
9.解下列不等式:
(1)![]() ≥0;(2)x(x-3)(x+1)(x-2)≤0
≥0;(2)x(x-3)(x+1)(x-2)≤0 ![]()
10. k为何值时,下式恒成立:![]()
能力提高
11.已知关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,则实数
,则实数![]() 的取值范围
的取值范围
是( )
(A)(-¥,1) (B)(2,+¥) (C)(1,2) (D)[1,2]
12.解关于![]() 的不等式
的不等式![]() ,
,![]()
3.2 一元二次不等式及其解法第1课时参考答案
例1.解:(I)根据实数运算的符号法则,可以化为不等式组求解.原不等式的解集是下面两个不等式组解集的并集:
(1)![]() (2)
(2)![]()
![]()
所以原不等式的解集是![]() 或
或![]() .
.
(II)原不等式等价于![]() 且
且 ![]() ,
,
∴原不等式的解为![]()
评注:一些较复杂的不等式,通常可转化为不等式组进行求解,但在解的过程中要注意
何时取交集,何时取并集.若将(2)改为![]() 呢?
呢?
 例2.解:(1)根据积的符号法
例2.解:(1)根据积的符号法![]() 则,可以将原不等式等价变形为
则,可以将原不等式等价变形为
(x2-3x+2)(x2-2x-3)<0
即(x+1)(x-1)(x-2)(x-3)<0
令(x+1)(x-1)(x-2)(x-3)=0
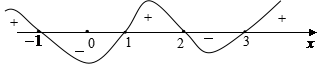
可得零点x=-1或1,或2或3,将数轴分成五部分(如图)![]()
由数轴标根法可得所求不等式解集为:
{x|-1<x<1或2<x<3}
(2)原不等式等价变形为:![]() -1>0
-1>0
 通分整理得:
通分整理得:![]() >0
>0
等价变形为:
(x2-2x+3)(x2-3x+2)>0
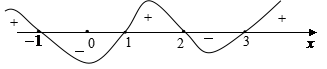
即 (x+1)(x-1)(x-2)(x-3)>0![]()
由数轴标根法可得所求不等式解集为:{x|x<-1或1<x<2或x>3}
例3.解:(1)原不等式可化为:![]()
即 ![]() 解之
解之 ![]() 或
或![]()
![]()
∴x>2或![]() ∴不等式的解集为{x|x>2或
∴不等式的解集为{x|x>2或![]() }
}![]()
(2)原不等式等价于 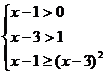 或
或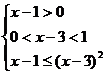
解之得 4<x≤5![]() ∴原不等式的解集为{x|4<x≤5}
∴原不等式的解集为{x|4<x≤5}![]()
评注:指数、对数不等式的处理原则,是转化为一般的不等式,如含参数,还要兼顾到底数的分类,按![]() 两种情况进行讨论。
两种情况进行讨论。
例4.解:(1)![]()
![]() ;
;
(2)原式变为![]() ,可化为
,可化为![]() ,
,
即![]() ,
,
当![]() 时,解集为
时,解集为![]() ;
;
当![]() 时,解集为
时,解集为![]() ;
;
当![]() 时,解集为
时,解集为![]() 。
。
评注:含有参变量的不等式,要注意分类讨论。
参考答案
1~5 BBCDB;
6.![]() ;7.
;7.![]() ;8.
;8.![]() ;
;
9.解:(1)![]() ≥0
≥0![]()
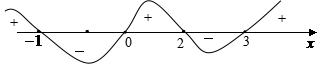
![]()
(2)x(x-3)(x+1)(x-2)≤0![]()
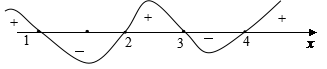
10.解:原不等式可化为:![]() ,而
,而![]()
∴原不等式等价于![]()
由![]() 得1<
得1<![]() k<3
k<3
11.C;提示:数形结合可知;
12.解:原不等式可化为![]() 。
。
①若![]() ,则
,则![]() ,不等式的解集为
,不等式的解集为![]() ;
;
②若![]() ,则不等式的解集为
,则不等式的解集为![]() ;
;
③若![]() ,则
,则![]() ,不等式的解集为
,不等式的解集为![]() ;
;
④若![]() ,则
,则![]() ,不等式的解集为
,不等式的解集为![]() 。
。
3.2 一元二次不等式及其解法
第3课时
学习目标
1.进一步提高解一元二次不等式的能力;
2.能运用三个“二次”的关系,解决恒成立、有解等问题,领会等价变形的思想。
要点精讲
1.若t>f(x)恒成立,则t>![]() ; 若t<f(x)恒成立,则t<
; 若t<f(x)恒成立,则t<![]() .(分离变量)
.(分离变量)
2.若t>f(x)有解,则t>![]() ;若 t<f(x)有
;若 t<f(x)有![]() 解,则t<
解,则t<![]() 。
。
范例分析
例1.已知函数f(x)=ax2+bx+c的图象过点(-1,0)是否存在常数a,b,c使不等式x≤f(x)≤![]() 对一切实数x都成立?若存在,求出a,b,c的值,若不存在,说明理由.
对一切实数x都成立?若存在,求出a,b,c的值,若不存在,说明理由.
例2.设函数![]()
(1) 若对于一切实数![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)若对于![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
例3.(1)对一切实数![]() ,函数
,函数![]() 有意义,求
有意义,求![]() 的取值范围;
的取值范围;
(2)若![]() 在区间
在区间![]() 上恒正,则
上恒正,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
例4.(1)设![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,
,![]() ,若不存在实数
,若不存在实数![]() 使得
使得![]() 和
和![]() 同时成立,试求实数
同时成立,试求实数![]() 的取值范围。
的取值范围。
规律总结
等价转化是把未知解的问题转化到在已有知识范围内可解的问题的一种重要的思想方法。通过不断的转化,把不熟悉、不规范、复杂的问题转化为熟悉、规范甚至模式化、简单化的问题。恒成立问题是高考考查的一个重要题型,数形结合与分离参量是解决恒成立问题的有效方法。
基础训练
一、选择题
1.已知![]() ,
,![]() ,当
,当![]()
![]()
![]() 时,
时,
![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若不等式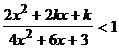 对
对![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
(A)(-¥,+¥) (B)(1,3) (C)(-¥,1) (D)(-¥,1)∪(3,+¥)
3.若不等式x2+ax+1 ³ 0对于一切xÎ(0,![]() 〕成立,则实数a的最小值是( )
〕成立,则实数a的最小值是( )
A.0 B. –2 C.-![]() D.-3
D.-3
4.当![]() 时,不等式
时,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.若关于![]() 的不等式
的不等式![]() 在
在![]() 内有解,则实数
内有解,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
6.若对任何实数![]() ,不等式
,不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
7.当不等式![]() 中恰好有一个解时,实数
中恰好有一个解时,实数![]() 的值是
的值是
8.满足![]() 的不等式
的不等式![]() 恒成立的
恒成立的![]() 的取值范围是___________.
的取值范围是___________.
三、解答题
9.如果![]() ,其中
,其中![]() ,
,
求![]() 的取值范围。
的取值范围。
10.若不等式x2-2ax+a+6>0在x∈[-2,2]上时总成立,求实数a的取值范围.
四、能力提高
11.已知![]() 且
且![]() ,
,![]() ,当
,当![]() 时均有
时均有![]() ,则实数
,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() ∪
∪![]() C.
C.![]() ∪
∪![]() D.
D.![]() ∪
∪![]()
12.已知函数![]() ,若存在实数
,若存在实数![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的最大值。
的最大值。
3.2 一元二次不等式及其解法第1课时参考答案
例1.解:易知f(1)=1.
于是由![]() 得
得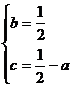 ,所以
,所以![]()
所以由![]() ,得
,得![]() 恒成立。
恒成立。
于是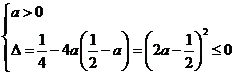 .所以
.所以![]() .
.
例2.(1)由![]() 恒成立,知
恒成立,知![]() ,或
,或![]() 且
且![]() ,得
,得![]() ;
;
(2)由![]() ,得
,得![]() 对一切
对一切![]() 恒成立,
恒成立,
由于![]() 在
在![]() 上的图象是线段,欲使
上的图象是线段,欲使![]() 恒成立,只需
恒成立,只需
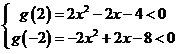 ,解得
,解得![]() 。
。
例3.(1)只需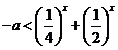 对一切实数
对一切实数![]() 恒成立,因为
恒成立,因为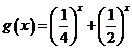 在
在![]() 上为减函数,所以
上为减函数,所以![]() ,故
,故![]() 。
。
(2)![]() 在
在![]() 上的图象是一条线段,
上的图象是一条线段,
由题意,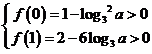 ,解得
,解得![]() ,选A。
,选A。
例4.解:(1)![]()
由![]() ,得
,得![]() 且
且![]() ,即
,即![]() 。
。
(2)由![]() 得
得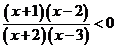 ,由数轴标根法知
,由数轴标根法知![]() ,
,
由![]() 知
知![]() ,由题意,
,由题意,![]() ,得
,得![]() 或
或![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() 或
或![]() 。
。
参考答案
1~5 CBCBA
3.提示:![]() 对一切xÎ(0,
对一切xÎ(0,![]() 〕成立,所以
〕成立,所以![]() ;
;
4.提示: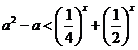 对一切
对一切![]() 恒成立,所以
恒成立,所以![]() ;
;
5.提示:因为![]() ,又
,又![]() 时,
时,![]() ,只需
,只需![]() 。
。
6.![]() ;
;
7.![]() ;提示:方程
;提示:方程![]() 恰有两个相等的实根,
恰有两个相等的实根,![]() ;
;
8.![]() 或
或![]() ;提示:
;提示:![]() 对一切
对一切![]() 恒成立,
恒成立,
只需![]() 且
且![]() 。
。
9.解:由![]() 得,
得,![]() 或
或![]() ,又
,又![]() ,
,
![]() ,得
,得![]() 或
或![]() ,
,
由已知,![]() ,得
,得![]() 。
。
10.解:令![]() ,
,
则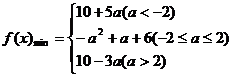
椐题意知由![]() 得
得![]() .
.
11.C;提示:只需![]() 对一切
对一切![]() 恒成立,数形结合,
恒成立,数形结合,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() 12.解:
12.解:![]() 对一切实数
对一切实数![]() 恒成立,只需
恒成立,只需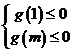 ,由
,由![]() 得
得![]() ,由
,由![]() 得
得
![]() ,所以存在最大值
,所以存在最大值![]() 符合条件。
符合条件。
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1