| 上传:admin | 审核发布:admin | 更新时间:2015-3-30 11:23:33 | 点击次数:805次 |
《二元一次不等式(组)与简单的线性规划问题》
一、 课标要求
1. 了解二元一次不等式(组)表示的平面区域和线性规划的意义.
2. 了解线性约束条件、线性目标函数、可行解、可行域、最优解等基本概念.
3. 了解线性规划问题的图解法,并能应用线性规划的方法解决一些简单的实际问题,以提
高解决实际问题的能力.
二、 本节重点和学习中可能遇到的困难
重点:从实际问题中抽象出二元一次不等式(组),二元一次不等式(组)表示的平面区域及简单的二元线性规划问题.
学习中可能遇到的困难:二元一次不等式表示的平面区域的探究过程及从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
三、 要点讲解
A.二元一次不等式(组)与平面区域
1.满足二元一次不等式(组)![]() 或
或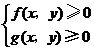 的
的![]() 和
和![]() 的取值构成有序实数对
的取值构成有序实数对![]() ,所有这样的有序实数对
,所有这样的有序实数对![]() 构成的集合称为二元一次不等式(组)的解.因为有序实数对
构成的集合称为二元一次不等式(组)的解.因为有序实数对![]() 可以看成直角坐标平面内点的坐标.所以,二元一次不等式(组)的解集是直角坐标系内的点构成的集合.
可以看成直角坐标平面内点的坐标.所以,二元一次不等式(组)的解集是直角坐标系内的点构成的集合.
2.在平面直角坐标系中,二元一次不等式![]()
![]() 在平面直角坐标系中表示直线
在平面直角坐标系中表示直线![]() 某一侧所有点组成的平面区域.当点
某一侧所有点组成的平面区域.当点![]() 在直线
在直线![]() 上时,
上时,![]() ;当点
;当点![]() 不在这条直线上时,则
不在这条直线上时,则![]() 或
或![]() .于是直线
.于是直线![]() 把平面分成两部分,此直线是这两部分平面区域的边界.若其中一部分平面的点用
把平面分成两部分,此直线是这两部分平面区域的边界.若其中一部分平面的点用![]() 表示,则
表示,则![]() 保持相同的符号;若另一部分平面上的点用
保持相同的符号;若另一部分平面上的点用![]() 表示,则
表示,则![]() 保持相同的符号且与前者符号相反.所以只需在此直线的某一侧取一个特殊点
保持相同的符号且与前者符号相反.所以只需在此直线的某一侧取一个特殊点![]() ,由
,由![]() 的正负即可判断
的正负即可判断![]() 表示的是直线哪一侧的平面区域.
表示的是直线哪一侧的平面区域.
特别地,当![]() 时,常有原点作为特殊点.
时,常有原点作为特殊点.
画不等式表示的平面区域是线性规划的入门知识,也是必备知识,其要点是“以线定界、以点(原点)定域”,同时还要注意哪条线应画成实线,哪条线应画成虚线.
例如:画出不等式![]() 的平面区域.
的平面区域.
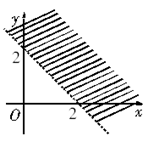 先作出边界
先作出边界![]() ,因为这条直线上的点都不满足
,因为这条直线上的点都不满足![]() ,故画成虚线;又因为
,故画成虚线;又因为![]() ,所以取原点
,所以取原点![]() 代入
代入![]() 得
得![]() ,所以,原点
,所以,原点![]() 不在
不在![]() 表示的平面区域内,其区域如图所示.
表示的平面区域内,其区域如图所示.
B.简单的线性规划问题
1.一般地说,求线性目标函数在线性约束条件下的最大值和最小值的问题,统称为线性规划问题.满足线性约束条件的解![]() 叫可行解,由所有可行解组成的集合叫做可行域.在可行域内存在使得线性目标函数取最大值或最小值的可行解叫做这个问题的最优解.
叫可行解,由所有可行解组成的集合叫做可行域.在可行域内存在使得线性目标函数取最大值或最小值的可行解叫做这个问题的最优解.
2.线性目标函数![]() 的几何意义:
的几何意义:![]() 是直线
是直线![]() 在
在![]() 轴上的截距.
轴上的截距.
3.生产实际中有许多问题都可以归纳为线性规划问题.在线性规划的实际问题中,主要掌握两种类型:一是给定一定数量的人力、物力资源,问怎样运用这些资源,能使完成的任务量最大,收到的效益最大;二是给定一项任务,问怎样安排,能使完成这项任务耗费的人力、物力资源最小.
4.求线性规划问题的步骤
图解法是解决线性规划问题的有效方法,其步骤是:①设未知数;②确定目标函数;③ 列出约束条件;④画出不等式(组)表示的平面区域,即可行域;⑤作平行直线系使之与可行域有交点;⑥求最优解并作答;⑦写出目标函数的最值.
四、 应注意的问题
1. 易错点:对可行域、最优解的判断出现问题或对目标函数的几何意义理解不清都容
易出现错误.
2. 课本习题中出现的线性规划都有唯一的最优解,其实线性规划的解有许多不同的情
况,除了有唯一的最优解的情况外,还有:
(1) 无可行解:这是约束条件组成的不等式组无解的情况;
(2) 有无穷多个最优解:这是目标函数![]() 和可行域的边界线平行的情况;
和可行域的边界线平行的情况;
(3) 有可行解,无最优解:这种情况只会出现在可行域是开区域的时候.如果线性
规划中的可行域是闭区域,那么一定有最优解.
3. 课本习题中出现的都是“截距型”目标函数![]() (
(![]() 不同时为零),即线
不同时为零),即线
性目标函数,高考中除了出现“截距型”目标函数的情况外,还有非线性目标函数:
(1)“斜率型”目标函数![]() (
(![]() 为常数).最优解为点(
为常数).最优解为点(![]() )与可行域
)与可行域
上的点的斜率的最值;
(2)“两点间距离型”目标函数![]() (
(![]() 为常数).最优解为点(
为常数).最优解为点(![]() )与可行域上的点之间的距离的平方的最值;
)与可行域上的点之间的距离的平方的最值;
(3)“点到直线距离型”目标函数![]() (
(![]() 为常数,且
为常数,且![]() 不同时为零).最优解为可行域上的点到直线
不同时为零).最优解为可行域上的点到直线![]() 的距离的最值.
的距离的最值.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

