福建省泉州十五中2014高中数学 3.4 基本不等式导学案1 新人教A版必修5

 学习目标 

学会推导并掌握基本不等式，理解这个基本不等式的几何意义，并掌握定理中的不等号“≥”取等号的条件是：当且仅当这两个数相等；

 

 学习过程 

一、课前准备

看书本97、98页填空

复习1：重要不等式：对于任意实数，有，当且仅当________时，等号成立. 

 

复习2：基本不等式：设，则，当且仅当____时，不等式取等号. 

 

二、新课导学

※ 学习探究

探究1：基本不等式的几何背景：

如图是在北京召开的第24界国际数学家大会的会标，会标是根据中国古代数学家赵爽的弦图设计的，颜色的明暗使它看上去象一个风车，代表中国人民热情好客. 你能在这个图案中找出一些相等关系或不等关系吗？

 

 

将图中的“风车”抽象成如图，

 

 

 

 

 

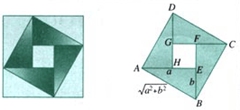
在正方形ABCD中有4个全等的直角三角形. 设直角三角形的两条直角边长为a，b那么正方形的边长为____________.这样，4个直角三角形的面积的和是___________，正方形的面积为_________.由于4个直角三角形的面积______正方形的面积，我们就得到了一个不等式：. 

当直角三角形变为等腰直角三角形，即a=b时，正方形EFGH缩为一个点，这时有_______________

 

结论：一般的，如果，我们有

当且仅当时，等号成立.

探究2：你能给出它的证明吗？

 

 

 

 

 

特别的，如果，，我们用、分别代替、，可得，

通常我们把上式写作：

 问：由不等式的性质证明基本不等？

用分析法证明：

证明：要证                (1)

只要证                        (2)

要证（2），只要证      （3）

要证（3），只 要证 （4） 

显然，（4）是成立的. 当且仅当a=b时，（4）中的等号成立. 

  3）理解基本不等式的几何意义

 

探究：课本第98页的“探究”

在右图中，AB是圆的直径，点C是AB上的一点，AC=a，BC=b. 过点C作垂直于AB的弦DE，连接AD、BD. 你能利用这个图形得出基本不等式的几何解释吗？

 

 

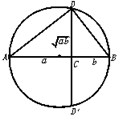
结论：基本不等式几何意义是“半径不小于半弦”

 

评述：

1.如果把看作是正数、的等差中项，看作是正数、的等比中项，那么该定理可以叙述为：两个正数的等差中项不小于它们的等比中项.

 

2.在数学中，我们称为、的算术平均数，称为、的几何平均数.本节定理还 可叙述为：两个正数的算术平均数不小于它们的几何平均数.

 

※ 典型例题 

例1 （1）用篱笆围成一个面积为100m的矩形菜园，问这个矩形的长、宽各为多少时，所用篱笆最短. 最短的篱笆是多少？

（2）段长为36 m的篱笆围成一个一边靠墙的矩形菜园，问这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少?

 

 

 

 

 

 

 

 

※ 动手试试

练1. 时，当取什么值时，的值最小？最小值是多少？

 

 

 

 

 

 

 

 

练2. 已知直角三角形的面积等于50，两条直角边各为多少时，两条直角边的各最小，最小值是多少？ 

 

 

 

 

 

 

三、总结提升

※ 学习小结

在利用基本不等式求函数的最值时，应具备三个条件：一正二定三取等号.

 

1. 已知x0，若x＋的值最小，则x为（    ）.

A． 81    B． 9    C． 3    D．16 

2. 若，且，则、、、中最大的一个是（    ）.

A．   B．   C．   D．

3. 若实数a，b，满足，则的最小值是（    ）.

A．18    B．6      C．     D．

4. 已知x≠0，当x=_____时，x2＋的值最小，最小值是________.

5. 做一个体积为32，高为2的长方体纸盒，底面的长为_______，宽为________时，用纸最少.

 

 课后作业 

1. （1）把36写成两个正数的积，当这两个正数取什么值时，它们的和最小？

（2）把18写成两个正数的和，当这两个正数取什么值时，它们的积最大？

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. 一段长为30的篱笆围成一个一边靠墙的矩形菜园，墙长18，问这个矩形的长、宽各为多少时，菜园的面积最大？最大面积是多少？