也谈高考数学立体几何题的审题策略

--一看二画三想四标识图

湖南省东安一中     唐志达  425900

 

    摘要:     

    高考数学立体几何题虽算中档题但确是部分考生,特别是以为”几何难学”的考生的心理障

碍题,压力大的题.求解速度慢且错了还不知道的题.本文通过”一看二画三想四标识”的图标

法,将已知条件图形化,带你去经历,去体会,去感受,轻轻松松复习好立体几何,考好立体几何题.

 

    关键词:一看、二画、三想、四标 识图

 

纵观近几年高考部分省市的高考试题,高考数学考查立体几何,一般是选择题2道,解答题一道,约占22分左右,解答题属于中档题.然而高考不同于平时练习作业,不允许考生用过多的时间去思考,要求学生必须在短时间内解决,这无疑增大了考生的心理压力和难度.怪不得部分考生是见到立体几何题就信心不足,茫然无从下手.做后也把握不住,最主要的原因就是看图不太懂,画图不清楚,想图犯迷糊.一句话就是空间构图和空间想象能力上不来,立体几何题的审题卡壳.毫不过分地说,对每一个立体几何题,加强”一看二画三想四标识图”的作图训练,这也是快速的提高审对审清立体几何题意,分析得出解题思路的关键一步.画好了将以知条件也图形化的立体图,也就等于完成了一半以上的解题工作.那么面对立体几何题考生应采取怎样的策略审题呢?

 

    一、通读、粗看

 

    面对一个立体几何题,开始读题是要通读(即泛读),只需搞懂题目大意,从整体上把握题意,防止出现”只见树林,不见森林”的怪圈,看图时也是一样,只需粗略的借助实物(如笔当直线,桌面当平面,桌的边当面内的直线,教室的上角有两两相交于一点的三条直线……)去看懂图的实虚立体感或抽象出一个基本空间图形来.

  例1：(2004年全国16)已知a,b为不垂直的异面直线,α是一个平面,则a,b在α上的射影有可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点;上面结论中正确的编号是______

 

开始读题时能读出“两条不垂直的异面直线a,b在面α的射影是什么形状的平面图?”就可以了.接下来应作的是,手拿两只笔当 a,b摆弄于桌上(演示,一看看,二画画,三想想,很明显图示就出来了:

 

 

 

对于(3)不可能出现,否则a,b就是共面了   故填①②④

 

    二、精读、画图、想图、标识、从而将已知条件图形化

   泛读,读懂题目的大意后,接下来就要精读,仔细搜索,捕捉.收集题中各种信息,抓出题中关关键的字、词、句,抓住图中关键的点、面、线,分清哪是已知条件,哪是可以分析得出的条件?本题要求解(证)的又是什么?精读还要画图、边读边画、边画边读、还要标识,将已知、分析出的条件标识到自己画的图上去(发现不理想,还要重画),按通常习惯,相等的线段点缀同样的记号(是数量值也可标数),相等的角也一样,直角有直角的记号,被遮的线要用虚线,中点线用M,N字母垂足常用H,O字母,平面的垂线通常画作与水平线垂直…….这是因为立体几何题常是叙述题图形的,通常都是以直观图表示立体图,除了与水平线平行的线段画等长外,其余都是“走了样”,考生经常出现看了后面忘前面的现象,因此在立体几何作图中不加以必要的精读和标识,就无法审对,审清题意,精读时要坚持饭一口一口地吃,将已知条件或分析得出的条件一点一点地标上图,这也就是通常所说的将已知条件图形化.

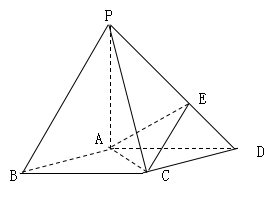
例2：(2004 湖南18) 如图，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=600，PA=AC=a，PB=PD=,点E在PD上，且PE:ED=1:1.

（I） 证明PA⊥平面ABCD；PB||面EAC

（II） 求以AC为棱，EAC与DAC为面的二面角的大小；

（III） 在棱PC上是否存在一点F，使BF//平面AEC？

证明你的结论.〈理科做〉

 

 

 

 

甲

通读时已经读出（1）要证线PA 面ABCD， 线PB// 面EAC，

               （2）找出并计算tan接下来精读并将已知条件图形代人上图甲

解：对于一个多问的题目，最好是抓住第一个问题人手，这是因为把所有的问题一起考虑，信息量加大了，不利于问题的解决，实际上，如果能够解决第一个问题，就说明已经理解题意了，从图甲中，易由勾股定理得，易知OE为中位线，从而第（1）问已解决；至于第（2）问，再作图乙，

可知EG//PA， EG=PA=a

GH=AG=，

故中，tan=

（详细解答省略）

  总之，高三立体几何的复习强调的是去经历、去体会、去感受，通过泛读精读，亲身实践，主动参与，真正地感受为求解而奋斗的喜怒哀乐，练习中注意把握“一看二画三想四标识图”的构图方法和审题策略，将已知条件图形化，几经总结和把握规律，你的看图能力，画图能力，想图能力将大幅度提高，以后面对高考将信心十足了。

 

 

 

 

    参考文献:

    （1）王晶  高考专题复习----立体几何  中学数学杂志2005(1)

         

    （2）曹炳友   度量二面角大小的基本思想方法   中学数学 2004(5)

         

    （3）艾为学   数学教学新课程标准     数学教学通讯 2004(1)