| 上传:蒋明生数学 | 审核发布:admin | 更新时间:2017-4-5 17:48:43 | 点击次数:614次 |
二次函数与一元二次方程
要点: 抛![]() 物线y=ax2+bx+c在x轴上的交点与一元二次方程ax2+bx+c
物线y=ax2+bx+c在x轴上的交点与一元二次方程ax2+bx+c![]() =0之间的关系:(1)如果抛物线与x轴___交点,那么一元二次方程___实数根;(2)如果抛物线与x轴只有___个交点,此时的交点就是抛物线的顶点,那么一元二次方程有两个___的实数根;(3)如果抛物线与x轴有___个交点,那么一元二次方程有两个___的实数根,此时,抛物线与x轴两个交点的横坐标x1,x2就是一元二次方程的两个实数根.
=0之间的关系:(1)如果抛物线与x轴___交点,那么一元二次方程___实数根;(2)如果抛物线与x轴只有___个交点,此时的交点就是抛物线的顶点,那么一元二次方程有两个___的实数根;(3)如果抛物线与x轴有___个交点,那么一元二次方程有两个___的实数根,此时,抛物线与x轴两个交点的横坐标x1,x2就是一元二次方程的两个实数根.
练习:1、 抛物线y=3x2+5x![]() 与两坐标轴交点的个数为___个.
与两坐标轴交点的个数为___个.
2、 下列哪一个函数,其图象与x轴有![]() 两个交点( )
两个交点( )
A y=![]() (x-23)2+155 B y=
(x-23)2+155 B y=![]() (x+23)2+155 C y=-
(x+23)2+155 C y=-![]() (x-23)2-155 D y=-
(x-23)2-155 D y=-![]() (x+23)2+155
(x+23)2+155
知识点1 二次函数与一元二次方程
1. 抛物线y=-3x2-x+4与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
2. 已知二次函数y=x2-3x+m(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程x2-3x+m=0的两实数根是( )
A.x1=1,x2=-1 B.x1=1,x2=2 C.x1=1,x2=0 D.x1=1,x2=3
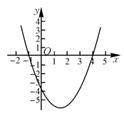
3. 小兰画了一个函数y=x2+ax+b的图象如图,则关于x的方程x2+ax+b=0的解是( )
A.无解 B.x=1 C.x=-4 D.x=-1或x=4
4. 抛物线y=2x2+8x+m与x轴只有一个公共点,则m的值为___
知识点2 利用二次函数求一元二次方程的近似解
5. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)一个解的范围是( )
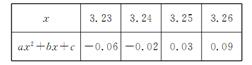
A.3<x<3.![]() 23 B.3.
23 B.3.![]() 23<x<3.24 C.3.24<x<3.25 D.3.25<x<3.26
23<x<3.24 C.3.24<x<3.25 D.3.25<x<3.26
6. 用图象法求一元二次方程2x2-4x-1=0的近似解.


第7题图 第9题图
知识点3 二次函数与不等式
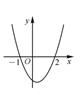
7. 二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是( )
A.x<-1 B.x>2 C.-1<x<2 D.x<-1或x>2
达标检测:
8. 已知抛物线y=x2-x-1与x轴的一个交点为(m,0),则代数式m2-m+2 014的值为( ![]() )
)
A.2 012 B.2 013 C.2 014 D.2 015
9. 抛物线y=ax2+bx+c(a<0![]() )如图所示,则关于x的不等式ax2+bx+c>0的解集是( )
)如图所示,则关于x的不等式ax2+bx+c>0的解集是( )
A.x<2 B.x>-3 C.-3<x<1 D.x<-3或x>1
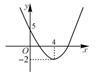
10. 二次函数y=ax2+bx![]() +c(a≠0,a,b,c为常数)的图象如图所示,ax2+bx+c=m有实数根的条件是( )
+c(a≠0,a,b,c为常数)的图象如图所示,ax2+bx+c=m有实数根的条件是( )
A.m≤-2 B.m≥-2 C.m≥0 D.m>4
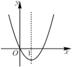
第10题图 第11题图
11. 二次函数y=x2+bx的图象如图,对称轴为直线x=1.若关于x的一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解,则t的取值范围是( )
A.t≥-1 B.-1≤t<3 C.-1≤t<8 D.3<t<8
12. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m
A.m 13. 抛物线y=2(x+3)(x-2)与 14. 已知二次函数y=x2-2mx+m2+3(m是常数). (1)
求证:不论m为何值,该函数的图象与x轴没有公共点; (2) 把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点? 15. 已知关于x的方程x2-(2k-3)x+k2+1=0有两个不相等的实数根x1、x2.
(1) 求k的取值范围; (2) 试说明x1<0,x2<0; (3) 若抛物线y=x2-(2k-3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OA·OB-3,求k的值. ![]() x轴的交点坐标分别为___.
x轴的交点坐标分别为___.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

