数学奥林匹克初中训练题6

第一试

一、选择题(每小题7分，共42分)

1.已知a²+b²=1，b²+c²=2，c²+a²=2.则ab+bc+ca的最小值为(    ).

(A)  -      (B)-  +      (C)-  -2    (D)  +

2.某次数学测验共有20道题.评分标准规定:每答对一题得5分，不答得0分，答错得-2分.已知这次测验中小强与小刚的累计得分相等，分数是质数.则小强与小刚答题的情况是(    ).

(A)两人答对的题数一样多         (B)两人答对的题数相差2

(C)两人答对的题数相差4          (D)以上三种情况都有可能

3.在△ABC中，AD是边BC上的中线，点M、N分别在边AB、AC上，且满足∠MDN=90°.如果BM²+CN²=DM²+DN²，那么，AD²与AB²+AC²的关系是(    ).

(A)AD²>AB²+AC²     (B)AD²2+AC²     (C)AD²=AB²+AC²    (D)AD²与AB²+AC²大小不确定

4.有n个数，从第二个数开始，每一个数都比它前面相邻的数大3，即4，7，…，3n+1，且它们相乘的积的末尾恰有32个0.则n的最小值为(    ).

(A)125      (B)126     (C)127     (D)128

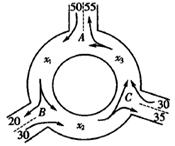5.图为某三岔路口交通环岛的简化模型.在某高峰时段，单位时间进出路口A、B、C的机动车辆数如图所示，图中的x₁、x₂、x₃分别表示该时段单位时间通过路段弧AB、BC、CA的机动车辆数(假设单位时间内，在上述路段中，同一路段上驶入与驶出的车辆数相等).则(    ).

(A)x₁>x₂>x₃     (B)x₁>x₃>x₂      (C)x₂>x₃>x₁    (D)x₃>x₂>x₁

6.已知四个互不相等的实数x₁、x₂、x₃、x₄(x₁2，x₃4).又a为实数，函数y₁=x²-4x+a与x轴交于(x₁，0)、(x₂，0)两点，函数y₂=x²+ax-4与x轴交于(x₃，0)、(x₄，0)两点.若这四个交点从左到右依次标为A、B、C、D，且AB=BC=CD，则a的值为(    ).

(A)a=-3      (B)a小于0       (C)a=0     (D)a大于0

二、填空题(每小题7分，共28分)

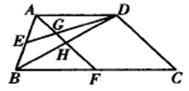1.如图，AD∥BC，梯形ABCD的面积是180，E是AB的中点，F是边BC上的点，且AF∥DC，AF分别交ED、BD于点G、H.设BC/AD=m(m∈N).若△GHD的面积为整数，则m的值为        .

2.将自然数1，2，…，k²列成正方形数表(如表1)，然后从表中任意选定1个数，随后删掉该数所在的行和列，再对剩下的(k-1)2个数的正方形数表作同样处理，如此下去，共作k次选数程序.则被选中的k个数之和       

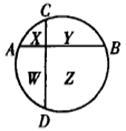3.如图，设AB、CD是以O为圆心、r为半径的圆的两条互相垂直的弦，且将圆分成的四个部分(每一部分允许退化为一个点)依顺时针顺序记为X、Y、Z、W.则的最大值(其中，S_U表示U的面积)为        .

4.一个人掷骰子，把每次掷得的数字加起来，如果超过20就停止.那么，当他停下来的时候，他最有可能掷得数字的总和是        .

第二试

一、(20分)已知二次函数y=x²+2mx-n².

(1)若此二次函数的图像经过点(1，1)，且记m，n+4两数中较大者为P，试求P的最小值;

(2)若m、n变化时，这些函数的图像是不同的抛物线，如果每条抛物线与坐标轴都有三个不同的交点，则过这三个交点作圆，证明:这些圆都经过同一定点，并求出该定点的坐标.

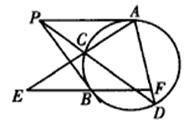
二、(25分)如图4，过圆外一点P作圆的两条切线PA、PB，A、B为切点，再过点P作圆的一条割线分别交圆于点C、D，过点B作PA的平行线分别交直线AC、AD于点E、F.求证:BE=BF.

三、(25分)设1≤a₁2<…n≤21是n个任意的整数.若其中总有4个不同的数a数a_i、a_j、a_k、a_m满足a_i+a_m=a_j+a_k(1≤i，则称数组(a₁，a₂，…，a_n)的阶数n为“好数”.

(1)n=7是否为好数?说明理由;

(2)n=8是否为好数?说明理由.