| 上传:蒋明生数学 | 审核发布:admin | 更新时间:2017-4-7 12:20:00 | 点击次数:874次 |
数学奥林匹克初中训练题7
第一试
一、选择题(每小题7分,共42分)
1.设a1,a2,…,an表示0~9的数字,且n+ 1位数![]() 乘以2后变为2a1a2…an.则n的最小值为( ).
乘以2后变为2a1a2…an.则n的最小值为( ).
(A)15 (B)16 (C)17 (D)18
2.时钟指在上午9时至10时的某一时刻,这一时刻前2分钟的时针与后2分钟的分针在一条直线上(不考虑重合情形).则这一时刻为( ).
(A)9时13![]() 分 (B)9时16分 (C)9时12分 (D)9时14分
分 (B)9时16分 (C)9时12分 (D)9时14分
3.五边形ABCDE中,∠A=∠C=90°,AB=BC=DE=AE+CD=3.则这个五边形的面积为( ).
(A)9 (B)10.5 (C)12 (D)13.5
4.对于每个x,函数y是函数y1=2x,y2=x+3,y3=-x+3中的最大值.则函数y的最小值为( ).
(A)2 (B)3 (C)5 (D)6
5.已知二次函数y=ax2+bx+c开口向下,顶点位于第二象限,且经过点(1,0)及(0,2).则a的取值范围是( ).
(A)a<0 (B)a<-1 (C)-2
6.设G是△ABC的重心,r是△ABC内切圆的半径,点G到边BC、CA、AB的距离分别为GD、GE、GF.令s=![]() .则( ).
.则( ).
(A)s>![]() (B)s=
(B)s=![]() (C)s<
(C)s<![]() (D)不能确定
(D)不能确定
二、填空题(每小题7分,共28分)
1.将分式![]() 写成分母分别为n、n+1、n+2、n+3的四个分式的代数和,结果为 .
写成分母分别为n、n+1、n+2、n+3的四个分式的代数和,结果为 .
2.已知a、b为正数,且2a+b=2.则![]() +
+![]() 的最小值为 .
的最小值为 .
3.已知实数a、b满足a2=-1-5a,5b=-1-b2.则![]() 的值为 .
的值为 .
4.已知AD是△ABC的内角平分线,AD的延长线交△ABC的外接圆于点E.则AB·AC-BD·DC与AD2的关系是 (填“相等”或“不相等”).
第二试
一、(20分)求不定方程29a+30b+31c=2 196的正整数解.
二、(25分)在凸四边形ABCD中,E、F分别是边AB、AD上的点,EF∥BD,过点E作EM⊥CD于点M,过点F作FN⊥BC于点N,且EM、FN、AC相交于同一点G.求证:AC⊥BD.
三、(25分)在△ABC中,已知
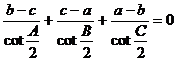 . 求证:
. 求证: 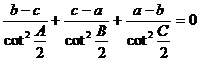
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

