| 上传:蒋明生数学 | 审核发布:admin | 更新时间:2017-6-2 13:56:49 | 点击次数:858次 |
教材的P11出现了一组美丽的几何图形,教材只对它的画法作了简单的说明,今天我们再次就其来源与变化,利用数据去分析它的内在本质.
科赫曲线是一种外形像雪花的几何曲线,所以又称为雪花曲线,雪花曲线因其形状类似雪花而得名,它的产生假定也跟雪花类似,它是分形曲线中的一种.
科赫曲线,是以数学家尼尔斯·冯·科赫来命名的,我们教材中的出现的曲线就是.科赫,出生于瑞典一个显赫的贵族家庭.冯·科赫的祖父曾担任瑞典的司法大臣,父亲是瑞典皇家近卫骑兵团的中校.研究数学和哲学,是当年瑞典贵族阶层的流行风尚,如今闻名世界的诺贝尔奖,就是由瑞典皇家科学院专设的评选委员会负责评审和颁发的.冯·科赫在1887年被新成立不久的斯德哥尔摩大学录取,师从著名的函数论专家哥斯塔·米塔格-列夫勒(Gösta Mittag-Leffler).由于斯德哥尔摩大学当时尚未获得颁发学位的许可,之后他又就读于乌普萨拉大学,在此校获得文学士及哲学博士学位之后,被斯德哥尔摩的皇家工学院任命为数学教授,在短短的54年生命中,冯·科赫写过多篇关于数论的论文.其中较突出的一个研究成果是他在1901年证明的一个定理,说明了黎曼猜想等价于素数定理的一个条件更强的形式.但是,他留给这个世界的最广为人知的成果,还应该是这个此文中所介绍的以他而命名的科赫曲线.
科赫曲线的作法:
由图1那样的等边三角形开始.然后把三角形的每条边三等分,并在每条边三分后的中段向外作新的等边三角形,但要像图2那样去掉与原三角形叠合的边.接着对每个等边三角形尖出的部分继续上述过程,即在每条边三分后的中段,像图3那样向外画新的尖形.不断重复这样的过程,便产生了雪花曲线.
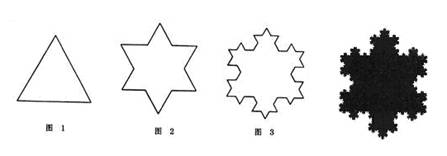
在产生科赫曲线的过程中,每一次变换都使得曲线的总长度变成原来长度的![]() 倍,也就是说乘以一个大于1的因子.例如,如果假设开始时的直线段长度为1,在图(a)中,折线总长度为
倍,也就是说乘以一个大于1的因子.例如,如果假设开始时的直线段长度为1,在图(a)中,折线总长度为![]() ;而图(b)的折线总长度为
;而图(b)的折线总长度为![]() ×
×![]() ;图(c)的折线总长度为
;图(c)的折线总长度为![]() ×
×![]() ×
×![]() ;这样一来,当变换次数趋向于无穷时,曲线的长度也趋向于无穷.
;这样一来,当变换次数趋向于无穷时,曲线的长度也趋向于无穷.
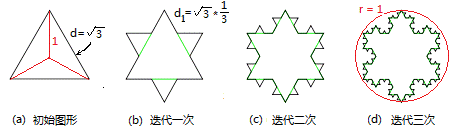
因为每条科赫曲线都是连续而无处可微的曲线,每条曲线的长度都是无限大,所以,由三条科赫曲线构成的科赫雪花的整个周长也应该是无限大.然而,从图中很容易看出,科赫雪花的面积却应该是有限的.因为整个雪花图形是被限制在一个有限的范围之内.比如,科赫雪花的面积应该是大于图(a)中正三角形的面积![]() ,而小于图(d)中红色圆形的面积:
,而小于图(d)中红色圆形的面积:![]() .
.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

