函数的奇偶性

1．函数f（x）=x(-1﹤x≦1)的奇偶性是                           （    ）

A．奇函数非偶函数                      B．偶函数非奇函数

C．奇函数且偶函数                      D．非奇非偶函数

2. 已知函数f（x）=ax²＋bx＋c（a≠0）是偶函数，那么g（x）=ax³＋bx²＋cx是(  ）

A.奇函数         B.偶函数

C.既奇又偶函数   D.非奇非偶函数

3. 若函数f(x)是定义在R上的偶函数，在上是减函数，

且f(2)=0，则使得f(x)<0的x的取值范围是 (   )  

A.(-¥,2)  B. (2,+¥)   C. (-¥,-2)È(2,+¥)   D. (-2,2)

4．已知函数f(x)是定义在(－∞,+∞)上的偶函数.

当x∈(－∞,0)时，f(x)=x-x⁴，则 当x∈(0.+∞)时，f(x)=             .

5. 判断下列函数的奇偶性：

(1)f(x)＝lg(-x);

(2)f(x)＝+

(3) f（x）=

6.已知g(x)=－x²－3,f(x)是二次函数，当x∈[-1,2]时，f(x)的最小值是1，且f(x)+g(x)是奇函数，求f(x)的表达式。

 

7.定义在（-1，1）上的奇函数f（x）是减函数，且f(1-a)+f(1-a²)<0,求a的取值范围

8.已知函数是奇函数,且上是增函数,

(1)求a,b,c的值;

(2)当x∈[-1,0)时,讨论函数的单调性.

9.定义在R上的单调函数f(x)满足f(3)=log3且对任意x，y∈R都有f(x+y)=f(x)+f(y)．

(1)求证f(x)为奇函数；

(2)若f(k·3)+f(3-9-2)＜0对任意x∈R恒成立，求实数k的取值范围．

 

10下列四个命题：

（1）f（x）=1是偶函数；

（2）g（x）=x³，x∈（－1，1是奇函数；

（3）若f（x）是奇函数，g（x）是偶函数，则H（x）=f（x）·g（x）一定是奇函数；

（4）函数y=f（|x|）的图象关于y轴对称，其中正确的命题个数是 （    ）

A．1         B．2          C．3           D．4

11下列函数既是奇函数，又在区间上单调递减的是(    )

A.   B. C.  D. 

12若y=f（x）（x∈R）是奇函数，则下列各点中，一定在曲线y=f（x）上的是（    ）

A．（a，f（－a））              B．（－sina，－f（－sina））     

C．（－lga，－f（lg））      D．（－a，－f（a））

13. 已知f（x）=x⁴+ax³+bx－8，且f（－2）=10，则f（2）=_____________。

14.已知是R上的奇函数，则a =      

15.若f(x)为奇函数，且在(-∞,0)上是减函数，又f(-2)=0，则xf(x)<0的解集为________

16.已知y=f(x)是偶函数，且在上是减函数，则f(1－x²)是增函数的区间是         

17.已知

（1）判断f（x）的奇偶性；

（2）证明f（x）>0。

 

 

 

 

 

答案

1.【提示或答案】 D

  【基础知识聚焦】掌握函数奇偶性的定义。

2.【提示或答案】A

  【基础知识聚焦】考查奇偶性的概念

3.【提示或答案】D

  【基础知识聚焦】考查奇偶性的概念及数形结合的思想

【变式与拓展】

1：f(x)是定义在R上的偶函数，它在上递减，那么一定有(  ）

A．    B． 

C．    D．

【变式与拓展】

  2：奇函数f(x)在区间[3，7]上递增，且最小值为5，那么在区间[－7，－3] 上是（   ）

A．增函数且最小值为－5

B．增函数且最大值为－5

C．减函数且最小值为－5

D．减函数且最大值为－5

4. 【提示或答案】f(x)=-x-x⁴

【变式与拓展】已知f（x）是定义在R上的奇函数，x>0时，f（x）=x²－2x+3，则f（x）=________________。

【基础知识聚焦】利用函数性质求函数解析式

5．【提示或答案】

 解(1)此函数的定义域为R.

∵f(-x)+f(x)＝lg(+x)+lg(-x)＝lg1＝0

∴f(-x)＝-f(x)，即f(x)是奇函数。

(2)此函数定义域为｛2｝，故f(x)是非奇非偶函数。

（3）∵函数f（x）定义域（－∞，0）∪（0，+∞），当x＞0时，－x＜0，

∴f（－x）=（－x）［1－（－x）］=－x（1+x）=－f（x）（x＞0）.

当x＜0时，－x＞0，∴f（－x）=－x（1－x）=－f（x）（x＜0）.

故函数f（x）为奇函数.

【基础知识聚焦】考查奇偶性的概念并会判断函数的奇偶性

6．解：设则

是奇函数

（1）当时，最小值为：

（2）当时,f(2)=1无解；

（3）当时，

  

综上得：或  

【基础知识聚焦】利用函数性质求函数解析式，渗透数形结合

7. 【提示或答案】     

-1<1-a<1 

-1<1-a²<1

f(1-a)<- f(1-a²)=f(a²-1),1-a> a²-1得0<a<1

【基础知识聚焦】考查奇偶性解决抽象函数问题

8．【提示或答案】

解(1)是奇函数，则

由,

由

又.

当

当a=1时,b=1,

【基础知识聚焦】结合具体函数，考查函数性质

9【提示或答案】

  分析：欲证f(x)为奇函数即要证对任意x都有f(-x)=-f(x)成立．在式子f(x+y)=f(x)+f(y)中，令y=－x可得f(0)=f(x)+f(-x)于是又提出新的问题，求f(0)的值．令x=y=0可得f(0)=f(0)+f(0)即f(0)=0，f(x)是奇函数得到证明．

(1)证明：

f(x+y)=f(x)+f(y)(x，y∈R)，  ①

令x=y=0，代入①式，得f(0+0)=f(0)+f(0)，即 f(0)=0．

令y=－x，代入①式，得 f(x-x)=f(x)+f(-x)，又f(0)=0，则有

0=f(x)+f(-x)．即f(-x)=-f(x)对任意x∈R成立，所以f(x)是奇函数．

(2)解：f(3)=log3＞0，即f(3)＞f(0)，又f(x)在R上是单调函数，所以f(x)在R上是增函数，又由(1)f(x)是奇函数．

f(k·3)＜-f(3-9-2)

=f(-3+9+2)，

k·3＜-3+9+2，

3-(1+k)·3+2＞0对任意x∈R都成立．令t=3＞0，问题等价于t-(1+k)t+2＞0对任意t＞0恒成立．

令f(t)=t²－(1+k)t+2,其对称轴

当时,f(0)=2>0,符合题意;

当时,对任意t>0,f(t)>0恒成立

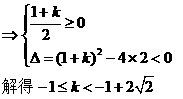
综上所述,所求k的取值范围是

【基础知识聚焦】考查奇偶性解决抽象函数问题，使学生掌握方法。

10【提示或答案】B

11【提示或答案】D

12【提示或答案】D

  【基础知识聚焦】掌握奇偶函数的性质及图象特征

13【提示或答案】6

【基础知识聚焦】考查奇偶性及整体思想

  【变式与拓展】：f（x）=ax³+bx－8，且f（－2）=10，则f（2）=_____________。

14【提示或答案】由f(0)=0得a=1

【基础知识聚焦】考查奇偶性。若奇函数f(x)的定义域包含，则f(0)=0；

f(x)为偶函数óf(x)=f(|x|)

15【提示或答案】画图可知，解集为;

16【提示或答案】x<-1,0<x<1

17【提示或答案】（1）偶函数 （2）x>0时，f(x)>0,x<0时-x>0,f(x)=f(-x)>0