7.2  坐标方法的简单应用

你喜欢旅游吗？给你一张风景区景点图，你会识图吗？你能用坐标准确地表示景点的位置吗？学习了本节知识，你就明白该怎么做啦！

【例1】如图6-2-1，某城市A地和B地之间经常有车辆来往，H地和D地间也经常有车辆来往.建立如图所示的直角坐标系，四地的坐标为：A(-3,2),D(1,1),H(-5,-3),B(-1,-4),拟建一座加油站，那么加油站建立在哪里对大家都方便，是给出具体的位置.

 

 

 

 

 

 

 

 

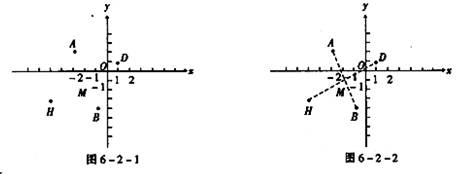
【点拨】关键是加油站建在何处对大家都方便，也就是大家都加油站距离较近，显然应建在两条道路的交叉点上较方便.

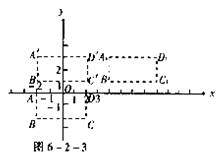【答案】加油站应建在点M(-2,-1)处，因为此处是道路与道路的交叉口，加油站建在此处对两条道路上的车加油都方便，结果如图6-2-2所示

   【例2】图6-2-3中，矩形ABCD沿y轴向上平移3个单位

后，得到矩形A′B′C′D′.四个顶点的坐标有什么变化呢？

若矩形A′B′C′D′再沿x轴向右平移6个单位后，得到的

矩形A₁B₁C₁D₁,四个顶点的坐标有什么变化呢？

   【点拨】关键是搞清平移方向.若沿x轴平移，则横坐标

变化而纵坐标不变；若沿y轴平移，则纵坐标变化而横坐标不变.

【答案】矩形ABCD的四个顶点的坐标是A(-2,0),B(-2,-2),C(2,-2),D(2,0);沿y轴平移后的矩形A′B′C′D′四个顶点的坐标是A′(-2,3),B′(-2,1),C′(2,1), D′(2,3);沿x轴平移后的矩形A₁B₁C₁D₁,四个顶点的坐标是A₁(4,3),B₁(4,1),C₁(8,1),D₁(8,3).

    1.如图6-2-4是公园平面示意图，试借助刻度尺、量角器解决下列问题并填空：荷花池

在大门的北偏西      度的方向上，到大门的距离为     厘米；马戏团在九曲桥的        度的方向上，到九曲桥的距离为       厘米.

2.人们给电脑屏幕上的点也建立了坐标系，如果电脑屏幕

左下方的点是(0,0）右上方的点的坐标是(720,600),要在屏幕

的中央画一个点，此点的坐标是         .

    1.如图6-2-5时效应所在学校的平面示意图，小英可以如何

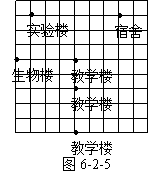描述他所住的宿舍位置呢？

 

 

 

 

 

 

 

 

 

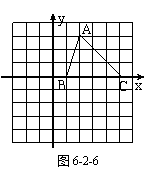2.如图6-2-6，△ABC沿x轴向作平移4个单位后得到△A₁B₁C₁，再作△A₁B₁C₁，关于x轴的轴对称图形，比较变化后的三角形的三个顶点的坐标有什么变化.

 

 

 

 

 

 

 

 

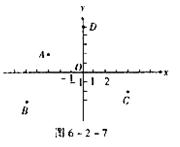
    1.如图6-2-7，某城市有4个牛奶供应站A(-3,2)、B(-5,-3)、C(4,-2)、D(0,5),现在建一个牛奶供应总站，总站建在AC与BD的交叉点上，你能确定总站的位置吗？

 

 

 

 

 

 

 

2.陈群同学要在电话中告诉同学如图6-2-8所示的图形，为了描述清楚，它使用了与本节有关的知识，你能猜到他用的什么方法吗？请详细叙述他的方法.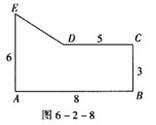

 

 

 

 

 

 

小华去某地考察环境污染问题，并且事先知道下面的信息：

①“悠悠日用化工品厂”在她现在所在地的北偏东30⁰、距离此处3km的地方；

②“加加调味品厂”在她现在所在地的北偏西45⁰、距离此处2.4km的地方；

③“幸福水枯”在她现在所在地的南偏东27⁰、距离此处1.5km的地方，根据这些信息，请建立直角坐标系，帮助小华完成这张表示各处位置的简图

 

 

 

 

 

 

 

 

 

 

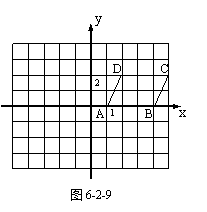如图6-2-9中的平行四边形ABCD做下列运动，画出相应的图形，指出四个顶点的坐标发生的变化.

(1)沿y轴正向平移2个单位；

(2)关于y轴对称；

(3)以点A为中心，将平行四边形ABCD旋转180⁰.

 

 

 

 

    平面上建立直角坐标系的木的使用(x,y)去表示点的位置.其实“坐标”也就是坐标标记

的意思.平面上除建立直角坐标系及点的位置外，还可建立各种各样的坐标系来标记点的位置，例如：极坐标系.

如果知道了一点M相对于以顶点O的距离和方向，那么这个点的位置就被惟一确定了，这就是说，我们可用角度和距离来确定平面上的点的相对位置.

在平面内取一个顶点O叫做极点，引一条射线O_X，叫做极轴，在选定一个长度单位和角度的正方向（通常取逆时针方向）.对于平面内任一点M，用ρ表示线段OM的长度，θ表示从O_X到OM的角度，ρ叫做点M的极径，θ叫做点M的极角，（注：θ用弧度制，180⁰=π，90⁰=，30⁰=，即1⁰=弧度），有序数对(ρ,θ)就叫做点M的极坐标.这样建立的坐标系叫做极坐标系.极坐标为ρ,θ的点M，可表示为M(ρ,θ).建立极坐标系后，给定ρ和θ，就可以在平面内惟一确定一点M.

问题：在直角坐标系xOy中，点A、B的坐标为：A(0,3)、B(4,0),若以O为极点，Ox为极轴，你能写出点A、B的极坐标吗？