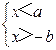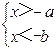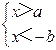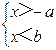| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-7-19 9:50:37 | 点击次数:977次 |
2013-2014学年甘肃省古浪四中七年级下学期期末考试数学试卷(带解析)
1、下列命题:①对顶角相等;②在同一平面内,垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中错误的有( )
|
A.1个 |
B.2个 |
C.3个 |
D.4个 |
【答案】B.
【解析】
试题分析:根据对顶角的性质和平行线的判定定理,逐一判断.
①是正确的,对顶角相等;
②正确,在同一平面内,垂直于同一条直线的两直线平行;
③错误,角平分线分成的两个角相等但不是对顶角;
④错误,同位角只有在两直线平行的情况下才相等.
故①②正确,③④错误,所以错误的有两个,
故选B.
考点:平行线的判定.
2、下列说法正确的是( )
|
A.-6是36的算术平方根 |
|
B.±6是36的算术平方根 |
|
C. |
|
D. |
【答案】D.
【解析】
试题分析:根据算术平方根的定义可知:6是36的算术平方根,![]() 是6的算术平方根.因此,A、B、C选项是错误的,
是6的算术平方根.因此,A、B、C选项是错误的,
故选D.
考点:算术平方根.
3、已知a>b>0,那么下列不等式组中无解的是( )
|
A. |
B. |
C. |
D. |
【答案】D.
【解析】
试题分析:根据不等式组的解集的判定知选项A、B、C的不等式组有解,选项D无解.
故选D.
考点:不等式组的解.
4、要使两点![]() 、
、![]() 都在平行于
都在平行于![]() 轴的某一直线上,那么必须满足( )
轴的某一直线上,那么必须满足( )
|
A. |
B. |
C. |
D. |
【答案】A.
【解析】
试题分析:要使两点P1(x1,y1)、P2(x2,y2)都在平行于y轴的某一直线上,那么必须满足x1=x2.
故选A.
考点:坐标与图形性质.
5、若25x2=16,则x的值为( )
|
A. |
B. |
C. |
D. |
【答案】A.
【解析】
试题分析:25x2=16,
x2=![]() ,
,
x=±![]() ,
,
故选A.
考点:平方根.
6、点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
|
A.(1,-8) |
B.(1,-2 ) |
C.(-6,-1 ) |
D.( 0 ,-1) |
【答案】C.
【解析】
试题分析:点A(-3,-5)向上平移4个单位,再向左平移3个单位得到点B,坐标变化为(-3-3,-5+4);则点B的坐标为(-6,-1).
故选C.
考点:坐标与图形变化——平移.
7、如果a>b,那么下列结论一定正确的是( )
|
A. |
B.3― |
C. |
D. |
【答案】B.
【解析】
试题分析:∵a>b,
∴-a<-b,
∴3-a<3-b;
故本题选B.
考点:不等式的性质.
8、不等式![]() 的负整数解有( )
的负整数解有( )
|
A.1个 |
B.2个 |
C.3个 |
D.无数个 |
【答案】A.
【解析】
试题分析:∵![]()
去分母得:x-7+1<3x-2
解得:x>-2
∴不等式的负整数解为:-1.
故选A.
考点:不等式的整数解.
9、下列调查中,适合采用全面调查(普查)方式的是( )
|
A.对漓江水质情况的调查 |
|
B.对端午节期间市场上粽子质量情况的调查 |
|
C.对某班50名同学体重情况的调查 |
|
D.对某类烟花爆竹燃放安全情况的调查 |
【答案】C.
【解析】
试题分析:A:漓江水污染的情况,由于范围较大,适合用抽样调查;故此选项错误;
B、对端午节期间市场上粽子质量情况的调查,数量较大;不容易掌控,适合抽样调查,故此选项错误;
C:对某班50名同学体重情况的调查,数量少,范围小,采用全面调查;故此选项正确;
D:对某类烟花爆竹燃放安全情况的调查,具有破坏性,应选择抽样调查;故此选项错误;
故选C.
考点:全面调查与抽样调查.
10、将100个数据分成8个组,如下表:则第六组的频数为( )

|
A.12 |
B.13 |
C.14 |
D.15 |
【答案】D.
【解析】
试题分析:根据表格,得
第六组的频数x=100-(11+14+12+13+13+12+10)=15.
故选D.
考点:频数与频率.
11、如图,直线AB、CD、EF相交于点O,若∠DOF=30°,∠AOE=20°,则∠BOC=_____.
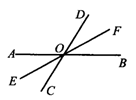
【答案】130°.
【解析】
试题分析:根据平角定义和∠DOF=30°,∠AOE=20°先求出∠AOD的度数,再根据对顶角相等即可求出∠BOC的度数.
试题解析:∵∠DOF=30°,∠AOE=20°,
∴∠AOD=180°-∠DOF-∠AOE=180°-30°-20°=130°,
∴∠BOC=∠AOD=130°.
考点:对顶角、邻补角.
12、如图,AB∥CD,∠1=64°,FG平分∠EFD,则∠EGF= °.
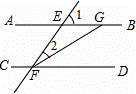
【答案】32°.
【解析】
试题分析:根据两直线平行,同位角相等求出∠EFD,再根据角平分线的定义求出∠GFD,然后根据两直线平行,内错角相等解答.
试题解析:∵AB∥CD,∠1=64°,
∴∠EFD=∠1=64°,
∵FG平分∠EFD,
∴∠GFD=![]() ∠EFD=
∠EFD=![]() ×64°=32°,
×64°=32°,
∵AB∥CD,
∴∠EGF=∠GFD=32°.
考点:平行线的性质.
13、若点M(2,a+3)与点N(2,2a-15)关于x轴对称,则a2+3=
【答案】19.
【解析】
试题分析:根据纵坐标互为相反数列式求得a的值,代入所给代数式求值即可.
试题解析:∵点M(2,a+3)与点N(2,2a-15)关于x轴对称,
∴a+3+2a-15=0,
解得a=4,
∴a2+3=19.
考点:1.关于x轴、y轴对称的点的坐标;2.代数式求值.
14、已知(a-2)2+|b+3|=0,则P(-a,-b)的坐标为
【答案】(-2,3).
【解析】
试题分析:根据非负数的性质,求出a,b的数值,可得P(-a,-b)的坐标.
试题解析:∵(a-2)2+|b+3|=0,
∴(a-2)2=0,|b+3|=0,
解得a=2,b=-3,
∴P(-a,-b)的坐标为(-2,3).
考点:1.点的坐标;2.绝对值;3.偶次方.
15、若x+2y+3z=10,4x+3y+2z=15,则x+y+z的值是 .
【答案】5.
【解析】
试题分析:把两个方程相加得到与x+y+z有关的等式而整体求解.
试题解析:将x+2y+3z=10与4x+3y+2z=15相加得5x+5y+5z=25,
即x+y+z=5.
考点:解三元一次方程组.
16、一个样本有100个数据,最大的350,最小的是75,组距为25,可分为_______组.
【答案】12.
【解析】
试题分析:根据组数=(最大值-最小值)÷组距计算,注意小数部分要进位.
试题解析:在样本数据中最大值为351,最小值为75,它们的差是351-75=276,已知组距为25,那么由于276÷25=11.04,故可以分成12组.
考点:频数(率)分布表.
17、若不等式组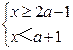 无解,则a的取值范围是
无解,则a的取值范围是
【答案】a≥2.
【解析】
试题分析:解出不等式组的解集(含a的式子),求出a的取值范围.
试题解析:因为不等式组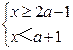 无解,
无解,
根据“大大小小解不了”则2a-1≥3,
∴a的取值范围是a≥2.
考点:解一元一次不等式组.
18、不等式5x-9≤3(x+1)的解集是________.
【答案】x≤6.
【解析】
试题分析:解不等式首先要去括号,然后移项合并同类项即可求得不等式的解集.
试题解析:不等式去括号,得
5x-9≤3x+3,
移项合并同类项,得
2x≤12,
系数化1,得
x≤6.
所以,不等式5x-9≤3(x+1)的解集是x≤6.
考点:解一元一次不等式.
19、已知![]() ,则
,则![]() = ,
= ,![]() = .
= .
【答案】2,3.
【解析】
试题分析:根据二次根式有意义的条件得到得
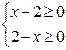 ,解得x=2,然后把x=2代入计算即可.
,解得x=2,然后把x=2代入计算即可.
试题解析:根据题意得
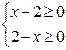 ,
,
解得x=2,
所以y=-3.
考点:二次根式有意义的条件.
20、为了了解某校2000名学生视力情况,从中测试了100名学生视力进行分析,在这个问题中,总体是__________,样本容量是__________。
【答案】某校2000名学生视力情况;100.
【解析】
试题分析:总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
试题解析:总体是:某校2000名学生视力情况;
样本容量是:100.
考点:总体、个体、样本、样本容量.
21、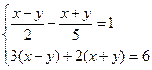
【答案】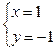 .
.
【解析】
试题分析:先把方程组进行整理,再求解即可.
试题解析:原方程组整理得: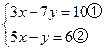
由②式得:y="5x-6" ③
把③式代入①式得:x=1.
把x=1代入③式得:y=-1.
所以方程组的解为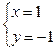 .
.
考点:解二元一次方程组.
22、解不等式组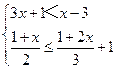 并写出它的整数解
并写出它的整数解
【答案】不等式组的解集为:-5≤x<-2.不等式组的整数解为:-5,-4,-3.
【解析】
试题分析:先解出不等式组的解集,再在解集范围内确定它的整数解即可.
试题解析: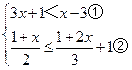
解不等式①得:x<-2;
解不等式②得:x≥-5.
∴不等式组的解集为:-5≤x<-2.
∴不等式组的整数解为:-5,-4,-3.
考点:1.解一元一次不等式组;2.一元一次不等式组的整数解.
23、已知:如图,AD∥BC,∠1=∠2。求证:∠3+∠4=180°。
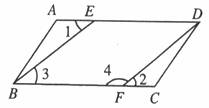
【答案】证明见解析.
【解析】
试题分析:欲证∠3+∠4=180°,需证BE∥DF,而由AD∥BC,易得∠1=∠3,又∠1=∠2,所以∠2=∠3,即可求证.
试题解析:∵AD∥BC,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BE∥DF,
∴∠3+∠4=180°.
考点:平行线的判定与性质.
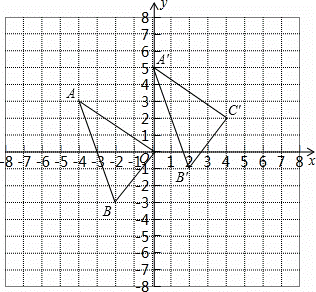
24、在平面直角坐标系中,已知点A(-4,3)、B(-2,-3)
(1)描出A、B两点的位置,并连结AB、AO、BO。
(2)△AOB的面积是__________。
把△AOB向右平移4个单位,再向上平移2个单位,画出平移后的△A′B′C′,并写出各点的坐标。
【答案】(1)画图见解析;(2)9;(3)画图见解析;A′(0,5),B′(2,-1),C′(4,2).
【解析】
试题分析:(1)根据平面直角坐标系找出点A、B的位置即可;
(2)利用△AOB所在的矩形的面积减去四周三个小直角三角形的面积,计算即可得解;
(3)找出平移后点A、B、O的对应点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标.
试题解析:(1)A、B两点的位置如图所示:
(2)△AOB的面积=4×6-![]() ×2×6-
×2×6-![]() ×2×3-
×2×3-![]() ×3×4
×3×4
=24-6-3-6
=24-15
=9;
(3)△A′B′C′如图所示,
A′(0,5),B′(2,-1),C′(4,2).
考点:作图-平移变换.
25、某厂共有120名生产工人,每个工人每天可生产螺栓25个或螺母20个,如果一个螺栓与两个螺母配成一套,那么每天安排多名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配成最多套?
【答案】每天安排可安排34名工人生产螺栓,86名工人生产螺母或每天安排可安排35名工人生产螺栓,85名工人生产螺母.
【解析】
试题分析:设每天安排多x名工人生产螺栓,y名工人生产螺母,根据共有120名工人及一个螺栓与两个螺母配成一套,可得出方程组,解出即可得出答案.
试题解析:设每天安排多x名工人生产螺栓,y名工人生产螺母,由题意得,
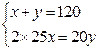 ,解得:
,解得: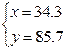 ,
,
若有34人生产螺母,则有86人生产螺栓,则每天生产850个螺栓,1720个螺母,生产850套;
若有35人生产螺母,则有85人生产螺栓,则每天生产875个螺栓,1700个螺母,生产850套
答:每天安排可安排34名工人生产螺栓,86名工人生产螺母或每天安排可安排35名工人生产螺栓,85名工人生产螺母.
考点:二元一次方程组的应用.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1