数学：18.1平行四边形同步测试题B（人教新课标八年级下）     

   A组

一、相信你的选择(每小题4分,共24分)

1．如图1，在平行四边形ABCD中，下列各式不一定正确的是          （  ）．

(A)      (B)

(C)      (D)

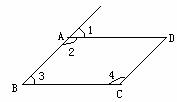
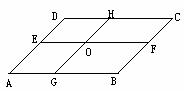
              图1                          图2

2．如图2，在□ABCD中，EF//AB，GH//AD，EF与GH交于点O，则该图中的平行四边形的个数共有                                                     （   ）.

(A)7 个    (B)8个    (C)9个    (D)11个

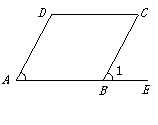
3．（08贵阳市）如图，在平行四边形中，是延长线上的一点，若，则的度数为（    ）

A．     B．     C．     D．

4．下列说法，属于平行四边形判别方法的有（     ）个.

①两组对边分别平行的四边形；②平行四边形的对角线互相平分；

③两组对边分别相等的四边形；④平行四边形的每组对边平行且相等；

⑤两条对角线互相平分的四边形是平行四边形；

⑥一组对边平行且相等的四边形是平行四边形．

(A)6个    (B)5个     (C)4个      (D)3个

5．如图3 ,在□ABCD中, ∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F的值为                                                               (    ).

(A)110°    (B)30°    (C)50°    (D)70°

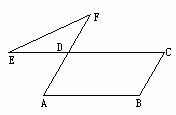
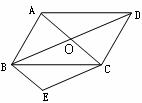
               图3                  图4

6．如图4，□ABCD中，对角线AC，BD相交于点O，将△AOD平移至△BEC的位置，则图中与OA相等的其它线段有                                       （    ）.

(A)1条      (B)2条      (C) 3条     (D) 4条

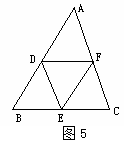
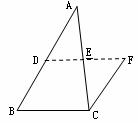
7．如图5，点D、E、F分别是AB、BC、CA边的中点，则图中的平行四边形一共有（  ）.

(A)1个    (B)2个    (C)3个   (D)4个

 

                                          

8．三角形三条中位线的长分别为3、4、5，则此三角形的面积为      （   ）.

 (A)12    (B)24    (C)36    (D)48

二、试试你的身手（每小题4分，共24分）

1．在平行四边形ABCD中，若∠A-∠B=70°，则∠A=_______，∠B=_______，

∠C=_______，∠D=_________．

2．在□ABCD中，AC⊥BD，相交于O，AC=6，BD=8，则AB=________，BC= _________．

3．如图6，已知□ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长是________．

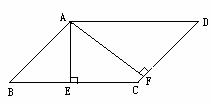
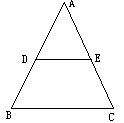
                  图6                    图7

4．如图7,△ABC中，D、E分别是AB、AC边的中点，且DE=6cm，则BC=__________．

5．用40cm长的长绳围成一个平行四边形，使长边与短边的比是3：2，则长边是____cm,短边是_____cm.

6.如图8,在ABCD中,AB=2cm，BC=3cm,∠B、∠C的平分线分别交AD于F、E，则EF的长为_____.

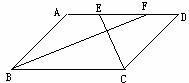
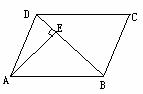
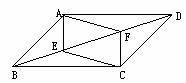
          图8                        图9                图10

7.如图9,□ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAC=_____度.

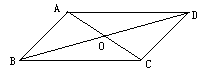
8.如图10，E、F是□ABCD对角线BD上的两点，请你添加一个适当的条件：     ，使四边形AECF是平行四边形．

三、、挑战你的技能(共52分)

1.(12分) 如图11，在□ABCD中，已知对角线AC和BD相交于点O，△AOB的周长为25，AB=12，求对角线AC与BD的和.

 

 

                                                 

图11

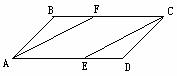2. (12分)如图12,在□ABCD中,已知点E和点F分别在AD和BC上,且AE=CF,连结CE和AF,试说明四边形AFCE是平行四边形.

                        

 

 

 

图12

3.(14分)如图13 ,□ABCD中，BD⊥AB，AB=12cm，AC=26cm，求AD、BD长．

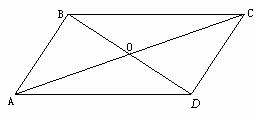
图13

4.(14分)如图14，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．

    求证：（1）⊿AFD≌⊿CEB．

   （2）四边形ABCD是平行四边形．

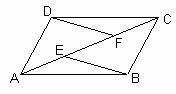
                              图14

 

 

 

(A)参考答案:

一、1.D  2.C  3.B  4.C  5.D  6.B  7.C  8.B

二、1.125°，55°，125°，55°;  2. 5, 5;    3. 3;  4. 12cm  ;  5.12, 8;  6.1;  7.20;  8. BE=DF．（或∠BAE=∠CDF等）.

三、1. 解：因为△AOB的周长为25，

所以OA+BO+AB=25，

又AB=12，所以AO+OB=25-12=13，

因为平行四边形的对角线互相平分，所以AC+BD=2OA+2OB=2(0A+OB)=2×13=26

2. 解:因为四边形ABCD是平行四边形,

所以AD//BC,

因为点E在AD上,点F在BC上,

所以AE//CF,

又因为AE=CF,

所以四边形AFCE是平行四边形.

3. 因为四边形ABCD是平行四边形，所以AO=CO=AC，OB=OD．

因为BD⊥AB，所以在Rt△ABO中，AB=12cm，AO=13cm．

所以BO=．所以BD=2B0=10cm．

所以在Rt△ABD中，AB=12cm，BD=10cm．

所以AD=(cm)．

4. （1）因为DF∥BE，  所以∠AFD＝∠CEB．  又因为AF=CE， DF=BE，

 所以△AFD≌⊿CEB．

（2）由(1)△AFD≌⊿CEB知AD=BC，∠DAF＝∠BCE ， 所以AD∥BC ，

所以四边形ABCD是平行四边形．

 

 

 

 

 

 

B组

一、相信你的选择(每小题6分,共24分)

1.如图1，△ABC中，∠ABC＝∠BAC，D是AB的中点，EC∥AB， DE∥BC，AC与DE交于点O．下列结论中，不一定成立的是                                 (   ).

(A)AC=DE        (B)AB=AC    (C)AD=EC        (D)OA=OE

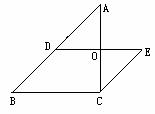
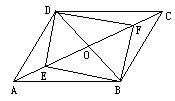
图1                图2

2.如图2，在□ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形               （    ）.

(A)AE=CF  (B)DE= BF  (C)∠ADE=∠CBF        (D)∠AED=∠CFB

3.已知点A（2，0）、点B（－，0）、点C（0，1），以A、B、C三点为顶点画平行四边形．则第四个顶点不可能在                                       （    ）.

(A)第一象限      (B)第二象限      (C)第三象限        (D)第四象限

4.如图3，O为□ABCD对角线AC、BD的交点，EF过点O且与边AD、BC分别交于点E、F，若BF=DE，则图中全等的三角形最多有                            （     ）.

(A)2对     (B)3对    (C)5对    (D)6对

                       图3

二、试试你的身手（每小题6分，共24分）

1.如图4，□ABCD的周长为16cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为_______．   

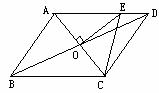
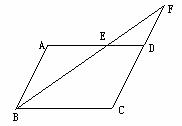
             图4                    图5

2.已知如图5，在平行四边形ABCD中，AB=4cm，AD=7cm，∠ABC的平分线交AD于点E，交CD的延长线于点F，则DF=     ___cm .

3.如图6,EF是△ABC的中位线,BD平分∠ABC交EF于D,DE=2,则EB=_____.

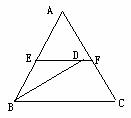
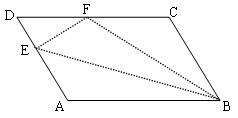
             图6                     图7

4. 如图7，□ABCD中，点E在边AD上，以BE为折痕，将△ABE向上翻折，点A正好落在CD上的点F，若△FDE的周长为8，△FCB的周长为22，则FC的长为_______.

三、挑战你的技能(共52分)

1.(17分)请写出使如图8所示的四边形ABCD为平行四边形的条件（例如，填：AB//CD且AD//BC，在不添加辅助线的情况下，写出除上述条件外的另外四组条件.

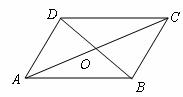
                     图8

2.(17分)工人师傅现在需要把一块三角形的铁板(如图9)，通过切割焊接成一个与其面积相等的平行四边形，你能帮助他设计一种可行的方案吗?请在图中画出焊接线，并说明你的理由．

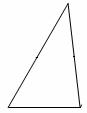
          图9

3.(18分)如图10， □ABCD中，E、F分别是边AD、BC上的点，请你自行规定E、F在边AD、BC上的位置，然后补充题设、提出结论并证明（要求：至少编制两个正确的命题，且补充题设不能相同）.

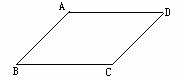
         图10               

 

 

(B)参考答案:<, /p>

一、1. B  2.B  3.C  4.D

二、1.8cm;  2.3;  3.2;  4.7

三、1. (1)∠DAB=∠DCB且∠ADC=∠ABC（或两组对角分别相等）；

　(2)AB=CD且AD=BC（或两组对边分别相等）；

　(3)OA=OC且OD=OB（或O是AC和BD的中点；或AC与BD互相平分；或对角线互相平分）；

(4)AD//BC且AD=BC（或AB//DC且AB=DC；或一组对边平行且相等）．

(5) AB//CD且∠DAB=∠DCB（或一组对边平行且一组对角相等）

2. 设计的方案如图所示，可分别取AB、AC边的中点D、E，连接DE，过点C作CF∥AB，交DE的延长线于F，把△ABC切割后，补在△CFE的位置上，就可焊接成□BCFD．理由如下：

 因为E是AC的中点， 所以AE=CE.

因为CF∥AB， 所以∠ADF＝∠F．

又因为∠AED＝∠CEF， 所以△ADE≌△CFE, 所以AD=CF．

因为D是AB的中点, 所以AD=BD，故BD=CF，

又因为CF∥AB，所以四边形BCFD是平行四边形．

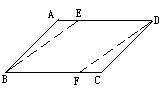3.  ①设AE=CF,如图(1),

已知□ABCD,AE=CF(补充条件)

求证:四边形EBFD是平行四边形(提出结论)

证明:连结BE、FD，

在□ABCD中，AD//BC，AD=BC，

又AE=CF，

所以ED//BF，ED=BF                           (1)

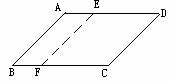所以四边形EBFD是平行四边形.

②设AE=BF.如图(2),

已知□ABFE是平行四边形,AE=BF(补充条件)

求证:四边形ABFE是平行四边形.

证明:连结EF.

因为四边形ABCD是平行四边形,                      (2)

所以AD//BC,AE//BF,                              

又AE=BF,

所以四边形ABEF是平行四边形.