| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-7-22 16:40:37 | 点击次数:807次 |
第十八章 四边形练习题
1. 如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( )

A.2![]() B.4
B.4![]() C.4 D.8
C.4 D.8
2. 下列命题中,真命题是( )
A.对角线相等的四边形是等腰梯形
B.对角线互相垂直且平分的四边形是正方形
C.对角线互相垂直的四边形是菱形
D.四个角相等的四边形是矩形
3. 如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.
其中正确的个数是( )

A. 0 B. 1 C. 2 D. 3
4. 如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF

5. 如图,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,下列结论不一定正确的是( )
A.AC=BD B.OB=OC C.∠BCD=∠BDC D.∠ABD=∠ACD

6. 如图,▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为 .

7. 如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ____________,使ABCD成为菱形.(只需添加一个即可)

8. 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .

9. 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,
则CD= .

10. 如图,□ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 .

11. 如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.

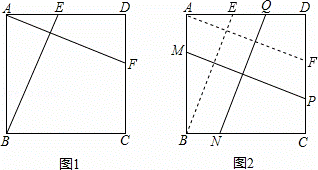
12. 如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.

13. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

14. 已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=____________时,四边形MENF是正方形(只写结论,不需证明)

15. 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.
(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.
(2)若AB∥CD,试证明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.

16. 如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,廷长BC到E,使得CE=AD,连接DE.
(1)求证:BD=DE.
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长.

答案
第十九章 四边形练习题
1. B 解析:∵AE为∠ADB的平分线,
∴∠DAE=∠BAE,
∵DC∥AB,
∴∠BAE=∠DFA,
∴∠DAE=∠DFA,
∴AD=FD,
又F为DC的中点,
∴DF=CF,
∴AD=DF=![]() DC=
DC=![]() AB=2,
AB=2,
在Rt△ADG中,根据勾股定理得:AG=![]() ,
,
则AF=2AG=2![]() ,
,
在△ADF和△ECF中,
 ,
,
∴△ADF≌△ECF(AAS),
∴AF=EF,
则AE=2AF=4![]() .
.
2. D 解析:对角线相等的四边形可能是等腰梯形、长方形、正方形等,所以A是假命题;对角线互相垂直且平分的四边形可能是正方形、菱形等,所以B是假命题;对角线互相垂直的四边形可能是菱形、正方形等,所以C是假命题;四个角相等的四边形是矩形是真命题.
3. D 解析:△ABC、△DCE是等边三角形,
∴∠ACB=∠DCE=60°,AC=CD,
∴∠ACD=180°﹣∠ACB﹣∠DCE=60°,
∴△ACD是等边三角形,
∴AD=AC=BC,故①正确;
由①可得AD=BC,
∵AB=CD,
∴四边形ABCD是平行四边形,
∴BD、AC互相平分,故②正确;
由①可得AD=AC=CE=DE,
故四边形ACED是菱形,即③正确.
综上可得①②③正确,共3个.
4. D 解析:∵EF垂直平分BC,
∴BE=EC,BF=CF,
∵CF=BE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
当BC=AC时,
∵∠ACB=90°,
∴∠A=∠EBC=45°
∴∠EBF=2∠EBC=2×45°=90°
∴菱形BECF是正方形.
故选项A正确,但不符合题意;
当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项B正确,但不符合题意;
当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项C正确,但不符合题意;
当AC=BD时,无法得出菱形BECF是正方形,故选项D错误,符合题意.
5. C 解析:A、∵四边形ABCD是等腰梯形,
∴AC=BD,
故本选项正确;
B、∵四边形ABCD是等腰梯形,
∴AB=DC,∠ABC=∠DCB,
在△ABC和△DCB中,
∵ ,
,
∴△ABC≌△DCB(SAS),
∴∠ACB=∠DBC,
∴OB=OC,
故本选项正确;
C、∵无法判定BC=BD,
∴∠BCD与∠BDC不一定相等,
故本选项错误;
D、∵∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABD=∠ACD.
故本选项正确.
6. 15 解析:∵□ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=CD,
∴OE=BC,
∴△DOE的周长=OD+OE+DE=BD+(BC+CD)=6+9=15,即△DOE的周长为15.
故答案是:15.

7. OA=OC或AD=BC或AD∥BC或AB=BC(答案不唯一)
8. (2,4)或(3,4)或(8,4) 解析:由题意,当△ODP是腰长为5的等腰三角形时,有三种情况:
(1)如答图①所示,PD=OD=5,点P在点D的左侧.

过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=![]() =
=![]() =3,
=3,
∴OE=OD-DE=5-3=2,
∴此时点P坐标为(2,4);
(2)如答图②所示,OP=OD=5.

过点P作PE⊥x轴于点E,则PE=4.
在Rt△POE中,由勾股定理得:OE=![]() =
=![]() =3,
=3,
∴此时点P坐标为(3,4);
(3)如答图③所示,PD=OD=5,点P在点D的右侧.

过点P作PE⊥x轴于点E,则PE=4.
在Rt△PDE中,由勾股定理得:DE=![]() =
=![]() =3,
=3,
∴OE=OD+DE=5+3=8,
∴此时点P坐标为(8,4).
综上所述,点P的坐标为:(2,4)或(3,4)或(8,4).
9. ![]() 解析:过点D作DE⊥BC于E.
解析:过点D作DE⊥BC于E.

∵AD∥BC,∠B=90°,
∴四边形ABED是矩形,
∴AD=BE=1,
∵BC=4,
∴CE=BC-BE=3,
∵∠C=45°,
∴CD=![]() .
.
10. ![]() 解析:∵四边形ABCD是平行四边形,BD=2,
解析:∵四边形ABCD是平行四边形,BD=2,
∴BE=![]() BD=1.
BD=1.
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,则BB′=![]() BE=
BE=![]() .
.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=![]() .
.

11. 证明:如图,过点B作BF⊥CE于F,
∵CE⊥AD,
∴∠D+∠DCE=90°,
∵∠BCD=90°,
∴∠BCF+∠DCE=90°,
∴∠BCF=∠D,
在△BCF和△CDE中, ,
,
∴△BCF≌△CDE(AAS),
∴BF=CE,
又∵∠A=90°,CE⊥AD,BF⊥CE,
∴四边形AEFB是矩形,
∴AE=BF,
∴AE=CE.

12. (1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,
∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF,
∵在△ABE和△DAF中,
 ,
,
∴△ABE≌△DAF(ASA),
∴AF=BE;
(2)解:MP与NQ相等.
理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,
由(1)可知MP=NQ.
13. 证明:(1)∵E是AD的中点,∴AE=ED.
∵AF∥BC,∴∠AFE=∠DBE, ∠FAE=∠BDE,
∴△AFE≌△DBE.
∴AF=DB.
∵AD是BC边上的中点,∴DB=DC,AF=DC
(2)四边形ADCF是菱形.
理由:由(1)知,AF=DC,
∵AF∥CD, ∴四边形ADCF是平行四边形.
又∵AB⊥AC, ∴△ABC是直角三角形
∵AD是BC边上的中线, ∴![]() .
.
∴平行四边形ADCF是菱形.
14. 解:(1)因为四边形ABCD是矩形,所以,∠A=∠D=90°,AB=DC,又MA=MD,
所以,△ABM≌△DCM
(2)四边形MENF是菱形;
理由:因为CF=FM,CN=NB,
所以,FN∥MB,同理可得:EN∥MC,
所以,四边形MENF为平行四边形,
又△ABM≌△DCM
∴MB=MC,又∵![]()
∴ME=MF,
∴平行四边形MENF是菱形.
(3)2:1
15. (1)证明:∵在△ABC和△ADC中 ,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
∵在△ABF和△ADF中 ,
,
∴△ABF≌△ADF,
∴∠AFD=∠AFB,
∵∠AFB=∠CFE,
∴∠AFD=∠CFE,
∴∠BAC=∠DAC,∠AFD=∠CFE.
(2)证明:∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)当EB⊥CD时,∠EFD=∠BCD,
理由:∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF,
在△BCF和△DCF中 ,
,
∴△BCF≌△DCF(SAS),
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠EFD=∠BCD.
16. (1)证明:∵AD∥BC,CE=AD,
∴四边形ACED是平行四边形,
∴AC=DE,
∵四边形ABCD是等腰梯形,AD∥BC,AB=DC,
∴AC=BD,
∴BD=DE.
(2)解:过点D作DF⊥BC于点F,

∵四边形ACED是平行四边形,
∴CE=AD=3,AC∥DE,
∵AC⊥BD,
∴BD⊥DE,
∵BD=DE,
∴S△BDE=![]() BD•DE=
BD•DE=![]() BD2=
BD2=![]() BE•DF=
BE•DF=![]() (BC+CE)•DF=
(BC+CE)•DF=![]() (BC+AD)•DF=S梯形ABCD=16,
(BC+AD)•DF=S梯形ABCD=16,
∴BD=4![]() ,
,
∴BE=![]() BD=8,
BD=8,
∴DF=BF=EF=![]() BE=4,
BE=4,
∴CF=EF-CE=1,
∴AB=CD=![]() =
=![]() .
.
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1

