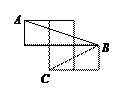| 上传:gxda147369 | 审核发布:admin | 更新时间:2015-8-7 16:10:04 | 点击次数:921次 |
 2013-2014学年下期期中考试卷
2013-2014学年下期期中考试卷
八年级数学
亲爱的同学,如果把这份试卷比作一片蔚蓝的海,那么,现在我们启航,展开你智慧和自信的双翼,乘风破浪,你定能收获无限……
一、精心选一选(每题3分,共24分)
1. 二次根式有意义,则x的取值范围是( )
A.x>1 B.x≥1 C.x<1 D.x≤1
2. 下列各式计算正确的是( )
C.![]() =
=![]()
![]() D.
D.![]()
3. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
A.90° B.60° C.45° D.30°
4. 如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( )
A.2条 B.4条 C.5条 D.6条
5. 如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于![]() AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.平行四边形
6. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)![]() 中正确的有( )
中正确的有( )
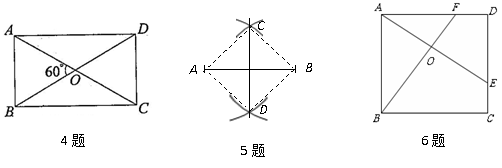 A. 4个 B. 3个 C. 2个 D. 1个
A. 4个 B. 3个 C. 2个 D. 1个
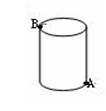 7.如图,在底面半径为2,(
7.如图,在底面半径为2,(![]() 取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
A.10 B.8 C.5 D.4
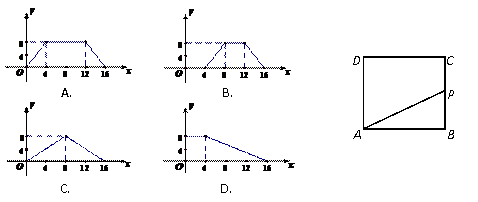
8. 如图,正方形ABCD的边长为4,P为正方形边上一动点,沿![]() 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
二、细心填一填(每题3分,共30分)
9. 若直角三角形的两直角边长为a、b,且满足![]() ,则该直角三角形的斜边长为 ______ .
,则该直角三角形的斜边长为 ______ .
10.如图所示,菱形ABCD中,对角线AC,BD相交于点O,H为AD边中点,菱形ABCD的周长为24,则OH的长等于________.
11. 实数![]() ,
,![]() 在数轴上的位置如图所示,则
在数轴上的位置如图所示,则![]() 的化简结果为____________.
的化简结果为____________.
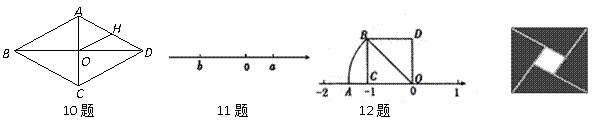 12.如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 。
12.如图,正方形ODBC中,OC=1,OA=OB,则数轴上点A表示的数是 。
13题
13. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽弦图它是由四全等的直
角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形 的面积是13,小正方形的面积是1,直角三角形的短直角边为a,较长直角边为b,下列说法:
①![]() ②
②![]() ③
③![]() ④
④![]()
其中正确结论序号是 __________
14. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,![]() 表示乌龟所行的路程,
表示乌龟所行的路程,![]() 表示兔子所行的路程).有下列说法:
表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1 000米;②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;④兔子和乌龟同时到达终点.
其中正确的说法是______________.(把你认为正确说法的序号都填上)
15. 如图,矩形![]() 沿着直线
沿着直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,AD=8,AB=6,则AE的长为 .
,AD=8,AB=6,则AE的长为 .
 16.在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和的最小值为______________
16.在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和的最小值为______________
14题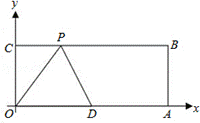
17.如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为__________________________
18. 如图,依次连结第一个矩形各边的中点得到一个菱形,再依次连结菱形各边的中点得到第二个矩形,按照此方法继续下去。已知第一个矩形的面积为1,则第n个矩形的面积为 。

三、认真算一算(11分)
19.(5分)![]()
20.(6分)先化简,再求值:![]() ,其中
,其中![]() .
.
四、耐心想一想(4小题,共35分)
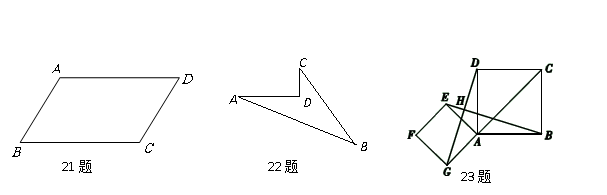
21. (7分)如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF.请再从下列三个备选条件中,选择添加一个恰当的条件,使四边形AECF是平行四边形,并予以证明.
备选条件:AE=CF,BE=DF,∠AEB=∠CFD.我选择添加的条件是: .
 (注意:请根据所选择的条件在答题卡相应试题的图中,画出符合要求的示意图,并加以证明)
(注意:请根据所选择的条件在答题卡相应试题的图中,画出符合要求的示意图,并加以证明)
22.(7分)我校要对如图所示的一块地进行绿化,已知AD=4m,CD=3m, AD⊥DC,AB=13m,BC=12m,求这块地的面积.
23.(9分)如图,点![]() 是正方形
是正方形![]() 对角线
对角线![]() 的延长线上任意一点,以线段
的延长线上任意一点,以线段![]() 为边作一个正方形
为边作一个正方形![]() ,线段
,线段![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
24. (12分)已知,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,垂足为
,垂足为![]() .
.
(1)如图24-1,连接![]() 、
、![]() .求证四边形
.求证四边形![]() 为菱形,并求
为菱形,并求![]() 的长;
的长;
(2)如图24-2,动点![]() 、
、![]() 分别从
分别从![]() 、
、![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周.即点
各边匀速运动一周.即点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止,点
停止,点![]() 自
自![]() →
→![]() →
→![]() →
→![]() 停止.在运动过程中,
停止.在运动过程中,
①已知点![]() 的速度为每秒5
的速度为每秒5![]() ,点
,点![]() 的速度为每秒4
的速度为每秒4![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求![]() 的值.
的值.
②若点![]() 、
、![]() 的运动路程分别为
的运动路程分别为![]() 、
、![]() (单位:
(单位:![]() ,
,![]() ),已知
),已知![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形,写出
四点为顶点的四边形是平行四边形,写出![]() 与
与![]() 满足的数量关系式.(直接写出答案,不要求证明)
满足的数量关系式.(直接写出答案,不要求证明)
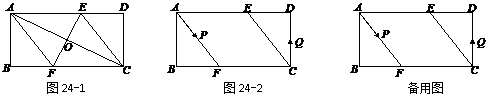
2013-2014学年下期八年级数学期中考试参考答案
一、精心选一选(每题3分,共24分)
1-5 BACDB 6-8 BAB
二、细心填一填(每题3分,共30分)
9. 5
10. 3 11. –b
12.![]()
![]()
![]() 13. ①④ 14. ①③
13. ①④ 14. ①③
15. ![]() 16.
16. ![]() 17. (2,4)(3,4)(8,4) 18.
17. (2,4)(3,4)(8,4) 18.![]()
三、认真算一算(11分)
19.解:原式=![]() ………………………3分
………………………3分
=4+![]() ………………………5分
………………………5分
20. ![]()
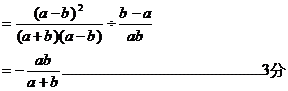
当![]() 时,
时,
原式=![]() ……………………………………6分
……………………………………6分
四、耐心想一想
21. 情形一:选择添加的条件是BE=DF 2分
证法一:∵四边形ABCD是平行四边形
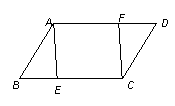 ∴AD=BC ,AD∥BC
∴AD=BC ,AD∥BC
∵BE=DF,
∴AD-DF=BC-BE 即 AF=CE
∴四边形AECF是平行四边形 7分
情形二:选择添加的条件是∠AEB=∠CFD 2分
证法一:∵四边形ABCD是平行四边形,
∴AD∥BC
∴∠AEB=∠EAF
又∵∠AEB=∠CFD,
∴∠EAF=∠CFD
∴AE∥CF
又∵AF∥EC,
∴四边形AECF是平行四边形 7分
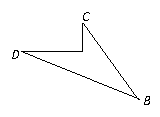 22.解:连接AC
1分
22.解:连接AC
1分
∵AD⊥DC
∴∠ADC=90°
在Rt△ADC中,根据勾股定理
![]() 3分
3分
在△ABC中,
∵![]()
根据勾股定理的逆定理,
△ ABC是直角三角形 6分
 ∴
∴![]() 7分
7分
23. (1)证明:(1) ∵四边形ABCD是正方形
∴AB=AD, ∠DAB=90°
∵四边形AEFG是正方形
∴AE=AG, ∠EAG=90°
∴∠DAB=∠EAG
∴∠DAB+∠EAD=∠EAG+∠EAD
即∠BAE=∠DAG
∴![]()
∴![]() …………………………………4分
…………………………………4分
(2)![]() ……………………………..5分
……………………………..5分
理由如下:
∵![]()
∴∠ABE=∠ADG
∵∠ABE+∠AKB=90°
∴ ∠ADG+∠AKB=90°
∵∠AKB=∠DKH
∴∠ADG+∠DKH=90°
∴∠DHK=90°
即![]() …………………………………..9分
…………………………………..9分
24.(1)证明:①∵四边形![]() 是矩形
是矩形
∴![]() ∥
∥![]()
∴![]() ,
,![]()
∵![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]()
∴![]()
∴![]() ≌
≌![]()
∴![]()
∴四边形![]() 为平行四边形
为平行四边形
又∵![]()
∴四边形![]() 为菱形……………………………4分
为菱形……………………………4分
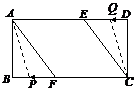 ②设菱形的边长
②设菱形的边长![]() ,则
,则![]()
在![]() 中,
中,![]()
由勾股定理得![]() ,解得
,解得![]()
∴![]() ………………………………………….6分
………………………………………….6分
(2)①显然当![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 上,此时
上,此时![]() 、
、![]() 、
、![]() 、
、![]() 四点不可能构成平行四边形;同理
四点不可能构成平行四边形;同理![]() 点在
点在![]() 上时,
上时,![]() 点在
点在![]() 或
或![]() 上,也不能构成平行四边形.因此只有当
上,也不能构成平行四边形.因此只有当![]() 点在
点在![]() 上、
上、![]() 点在
点在![]() 上时,才能构成平行四边形
上时,才能构成平行四边形
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]()
∵点![]() 的速度为每秒5
的速度为每秒5![]() ,点
,点![]() 的速度为每秒4
的速度为每秒4![]() ,运动时间为
,运动时间为![]() 秒
秒
∴![]() ,
,![]()
∴![]() ,解得
,解得![]()
∴以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]() 秒……….10分
秒……….10分
② ![]() 与
与![]() 满足的数量关系式是
满足的数量关系式是![]()
![]() ………12分
………12分
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1