数学因运动而充满活力，数学因变化而精彩纷呈。动态题是近年来中考的的一个热点问题，以运动的观点探究几何图形的变化规律问题，称之为动态几何问题，随之产生的动态几何试题就是研究在几何图形的运动中，伴随着出现一定的图形位置、数量关系的“变”与“不变”性的试题，就其运动对象而言，有点动、线动、面动三大类，就其运动形式而言，有轴对称（翻折）、平移、旋转（中心对称、滚动）等，就问题类型而言，有函数关系和图象问题、面积问题、最值问题、和差问题、定值问题和存在性问题等。解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况。以动态几何问题为基架而精心设计的考题，可谓璀璨夺目、精彩四射。

   动态几何形成的函数关系和图象问题是动态几何中的基本问题，包括单动点形成的函数关系和图象问题，双（多）动点形成的函数关系和图象问题，线动形成的函数关系和图象问题，面动形成的函数关系和图象问题。本专题原创编写线动点形成的函数关系问题模拟题。

线动问题就是在一些基本几何图形上，设计一个动线（包括平移和旋转），或由点动、面动形成线动，并对线在运动变化的过程中产生的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等进行研究。

在中考压轴题中，线动形成的函数关系问题的重点和难点在于应用数形结合的思想准确地进行分类。

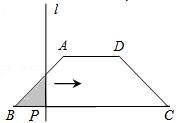
原创模拟预测题1. 如下图所示，已知等腰梯形ABCD，AD∥BC，AD=2，BC=6，AB=DC=，若动直线l垂直于BC，且从经过点B的位置向右平移，直至经过点C的位置停止，设扫过的阴影部分的面积为S，BP为x，则S关于x的函数关系式是          。

【答案】。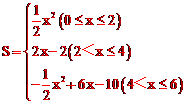

【考点】动线问题的函数图象，等腰梯形的性质，等腰直角三角形的判定和性质，分类思想的应用。

【分析】如图1，分别过点A，D作BC的垂线，垂足为E，F，

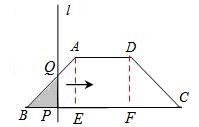
①如图1，当直线l经过BA段时，0≤x≤2，BP=QP=x，

。

②如图2，当直线l经过AD段时，2＜x≤4，BP=QP=x，AQ=EP=，

。

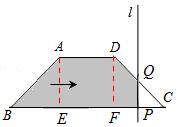
③如图3，当直线l经过DC段时，4＜x≤6，BP =x，FC=QP=，

。

综上所述，S关于x的函数关系式是。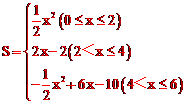

原创模拟预测题2. 把直线沿x轴方向平移m个单位后，与直线的交点在第一象限，则m的取值范围是【    】

A．      B．       C．       D．

【答案】A。

【考点】一次函数图象与平移变换，平面直角坐标系中各象限点的特征，解一元一次不等式组。

故选A。

原创模拟预测题3. 为了考察冰川融化的状况，一支科考队在某冰川上设定一个以大本营O为圆心，半径为4km 圆形考察区域，线段P₁、P₂是冰川的部分边界线（不考虑其它边界），当冰川融化时，边界线沿着与其垂直的方向朝考察区域平行移动.若经过n年，冰川的边界线P₁P₂移动的距离为s（km），并且s与n（n为正整数）的关系是.以O为原点，建立如图所示的平面直角坐标系，其中P₁、P₂的坐标分别是（－4，9）、（－13，－3）.

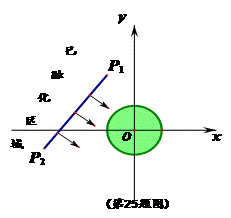
（1）求线段P₁P₂所在的直线对应的函数关系式；

（2）求冰川的边界线移动到考察区域所需要的最短时间.

【答案】（1）；（2）6．

【解析】

（2）在中，当，则，当，则，

∴与x、y轴的交点坐标是（0，）、（，0），由勾股定理，得，

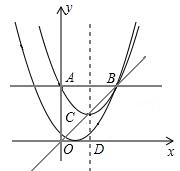
原创模拟预测题4. 如图，抛物线与y轴相交于点A，与过点A平行于x轴的直线相交于点B（点B在第一象限）．抛物线的顶点C在直线OB上，对称轴与x轴相交于点D。平移抛物线，使其经过点B、D，则平移后的抛物线的解析式为　    　。

【答案】。　

【考点】待定系数法，曲线上点的坐标与方程的关系，二次函数的性质。

∴对称轴为直线x=。∴点D的坐标为（，0），点B的坐标为（3，）。

设平移后的抛物线的解析式为y=x²+mx+n，

则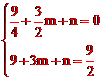，解得。

∴平移后的抛物线的解析式为。　

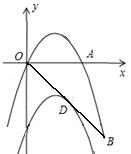
原创模拟预测题5. 如图，已知抛物线y=ax²+bx（a≠0）经过A（3，0）、B（4，）两点。

（1）求抛物线的解析式；

（2）将抛物线向下平移m个单位长度后，得到的抛物线与直线OB只有两个公共点D，求m的取值范围。

【答案】（1）∵抛物线y=ax²+bx（a≠0）经过A（3，0）、B（4，）

∴将A与B两点坐标代入得：，解得：。

∴抛物线的解析式是。

（2）设直线OB的解析式为y=k₁x，由点B（4，），得：=4k₁，解得：k₁=。

∴直线OB的解析式为y=x。

∵抛物线向下平移m个单位长度后的解析式为：。

∵点D在直线OB上，∴可设D（x，x）。

又∵点D在直线上，∴，即。

∵抛物线与直线有两个公共点，∴，解得：m＜4。

【考点】曲线平移问题，曲线上点的坐标与方程的关系，一元二次方程根的判别式，

原创模拟预测题6.如图1，在平面直角坐标系中，直线AB与轴交于点A，与轴交于点B，与直线OC：交于点C．

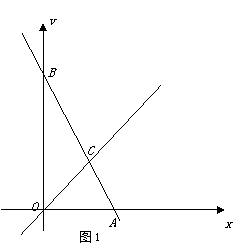
（1）若直线AB解析式为，

①求点C的坐标；

②求△OAC的面积．

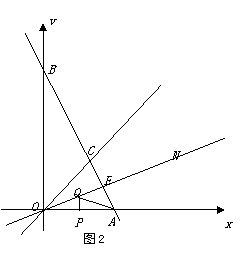
（2）如图2，作的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．

【答案】（1）①C（4，4）；②12；（2）存在，3

【解析】

（1）①由题意，  

解得所以C（4，4）；

②把代入得，，所以A点坐标为（6，0），

所以；

（2）由题意，在OC上截取OM＝OP，连结MQ

 

考点：一次函数的综合题

点评：本题知识点多，具有一定的综合性，要求学生具备一定的数学解题能力，有一定难度．