| 上传:席俊雄数学 | 审核发布:admin | 更新时间:2015-10-20 15:42:00 | 点击次数:577次 |
上课时间:2015年 月 日 学期总第 课时
|
课 题 |
函数的图象 |
课 型 |
复习课 |
||||
|
课 时 |
第 1 课时 |
主备课人 |
周思 |
||||
|
复备课人 |
陈雄武 |
审核人 |
雷淇未 |
||||
|
课前准备 |
|
||||||
|
教 学 目 标 |
1.在实际情境中会根据不同的需要选择函数的表示方法 2.会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式解的问题 |
||||||
|
教学重点 |
会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式解的问题 |
||||||
|
教学难点 |
函数图象的灵活运用 |
||||||
|
教学过程和教学内容 |
二次备课 |
||||||
|
一、基础回扣 1、函数图象的作图方法:
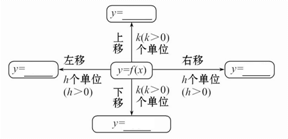
2、三种图象变换: (1)平移变换
(2)对称变换
③y=f(x) y= _______;
(3) 翻折变换: ①y=f(x) ②y=f(x)
①y=f(x) y= ______;
②y=f(x) y= ______. 二、典例突破 考向 1 作函数的图象 【典例1】作出下列函数的图象: (1)y=|log2(x+1)|. (2)y=(1/2)|x|. (3)y=
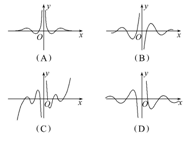
考向 2 识图与辨图 【典例2】(1)已知y=f(2x+1)是偶函数,则函数y=f(2x)的图象的对称轴是 (A)x=1 (B)x=-1 (C)x=-1/2 (D)x=1/2 (2)函数y=
考向 3 函数图象的应用 【典例3】已知函数f(x)=x|m-x|(x∈R),且f(4)=0. (1)求实数m的值. (2)作出函数f(x)的图象并判断其零点个数. (3)根据图象指出f(x)的单调递减区间. (4)根据图象写出不等式f(x)>0的解集. (5)求集合M={m|使方程f(x)=m有三个不相等的实根}.
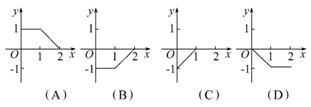
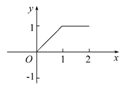
【易错误区】图象变换不正确或识图方法不当致误 【典例】(2012·湖北高考)已知定义在区间[0,2]上的函数y=f(x)的图象如图所示,则y= -f(2-x)的图象为 ( )
四、课时作业 |
|
||||||
|
教学札记: |
|||||||
东安一中教务处设计
通讯地址: 广州市天河区东圃黄村龙怡苑 (510660)邮箱:lzm6308@163.com 联系QQ:534386438
Copyright © 2008-2012 klxkc.com All Rights Reserved. 粤ICP备15026984号-1